本文主要包括堆的原理介绍和代码实现
具体的数据结构:数组、链表
抽象的数据结构:二叉树、队列、栈、优先队列、堆等
堆:是一种抽象的数据结构,我们在插入或删除元素后堆将自动调整结构以维持有序,可用二叉树实现。
优先队列 :是一种抽象的数据结构,在队列的基础上定义了元素的优先级,可用堆实现。
堆排序 :使用数据结构堆实现的排序算法。
因此,优先队列与堆排序
相同点:都使用了堆。
不同点:优先队列是数据结构,堆排序是排序算法。
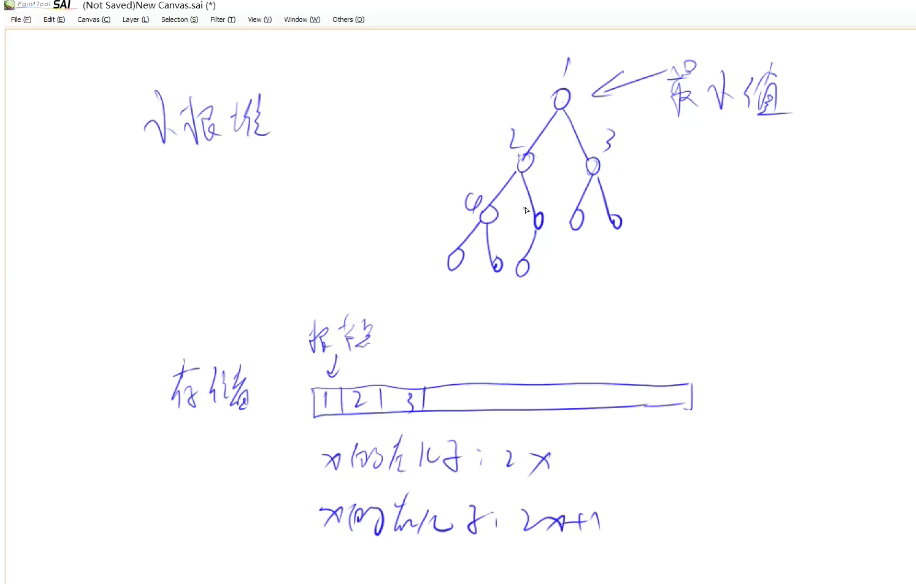
首先,堆是一个完全二叉树。知识点备忘
本次讨论的默认是小根堆 。(即每一个根结点的值小于等于其左右孩子节点的值)
使用一维数组来存储,一个节点编号为 x x x 2 x 2x 2 x 2 x + 1 2x+1 2 x + 1
为了编程方便,用数组存储时,下标也从1 1 1
向下调整 ,将一个节点向下移动,d o w n ( ) down() d o w n ( )
向上调整 ,将一个节点向上移动,u p ( ) up() u p ( )
一个节点的值变小了,向上移动,不断与父节点比较,交换。 heap[++ size] = x; up(size);
在整个堆的最后一个位置插入x,然后不断向上移动。
return heap[1];
将堆的最后一个元素覆盖到heap[1],size–,然后向下调整
heap[1] = heap[size]; size --; down(1);
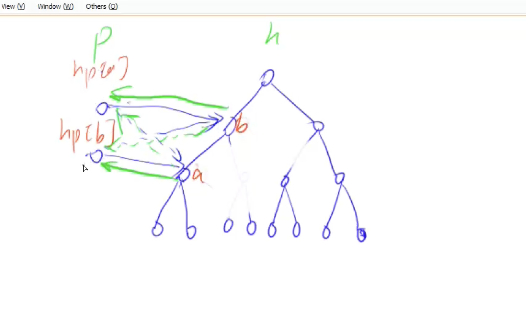
先将堆的最后一个元素覆盖到要删除的元素,如果变大了,就向下调整;变小了,就向上调整。
这里其实,可以不用管变大还是变小。直接先down,后up。实际两个过程只会执行一个。
heap[k] = heap[size]; size --; down(k); up(k);
先修改目标元素,然后down、up。
heap[k] = newVal; down(k); up(k);
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 const int N = 1e5 +10 ;int h[N];int cnt; void down (int u) int t = u; if (u * 2 <= cnt && h[u * 2 ] < h[t]) t = u * 2 ; if (u * 2 + 1 <= cnt && h[u * 2 + 1 ] < h[t]) t = u * 2 + 1 ; if (u != t) { swap (h[u], h[t]); down (t); } }
1 2 3 4 5 6 7 8 void up (int u) while (u / 2 > 0 && h[u] < h[u / 2 ]) { swap (h[u], h[u / 2 ]); u >>= 1 ; } }
从n/2开始down到0
1 for (int i = n / 2 ; i >= 1 ; -- i) down (i);
时间复杂度为O ( n ) O(n) O ( n )
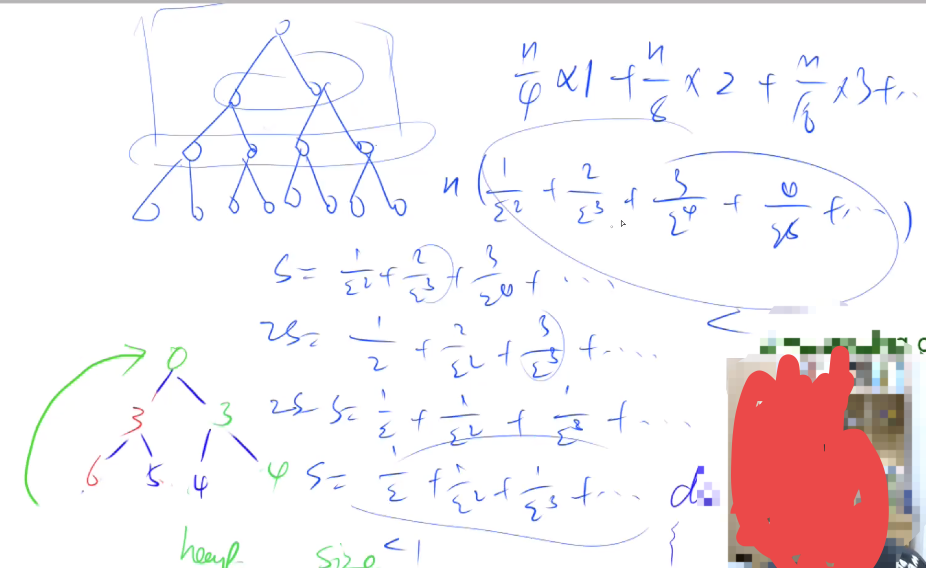
假设是满二叉树情况,进行复杂度的分析。
此时,h[n/2]的节点是倒数第二层最后一个节点,从倒数第二层开始
倒数第二层有 n 4 \frac{n}{4} 4 n d o w n ( k ) down(k) d o w n ( k ) n 4 × 1 \frac{n}{4}\times1 4 n × 1
倒数第三层有 n 8 \frac{n}{8} 8 n d o w n ( k ) down(k) d o w n ( k ) n 8 × 2 \frac{n}{8}\times2 8 n × 2
所以总的计算次数:
C N T = n 2 2 × 1 + n 2 3 × 2 + n 2 4 × 3 + ⋯ = n × ( 1 2 2 + 2 2 3 + 3 2 4 + ⋯ ) CNT = \frac{n}{2^2}\times1+\frac{n}{2^3}\times2+\frac{n}{2^4}\times3+\cdots=n\times(\frac{1}{2^2}+\frac{2}{2^3}+\frac{3}{2^4}+\cdots) C N T = 2 2 n × 1 + 2 3 n × 2 + 2 4 n × 3 + ⋯ = n × ( 2 2 1 + 2 3 2 + 2 4 3 + ⋯ )
S = 1 2 2 + 2 2 3 + 3 2 4 + ⋯ S=\frac{1}{2^2}+\frac{2}{2^3}+\frac{3}{2^4}+\cdots S = 2 2 1 + 2 3 2 + 2 4 3 + ⋯
S = 2 S − S = 1 2 + 1 2 2 + 1 2 3 + ⋯ ≤ 1 S=2S-S=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\cdots\le 1 S = 2 S − S = 2 1 + 2 2 1 + 2 3 1 + ⋯ ≤ 1
C N T ≤ n × 1 = n CNT≤n\times1=n C N T ≤ n × 1 = n
这里也可以用级数的知识去做
输入一个长度为 n n n m m m
只用到了向下调整down(k)
输入格式
第一行包含整数 n n n m m m
第二行包含 n n n
输出格式
共一行,包含 m m m m m m
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 #include <iostream> using namespace std;const int N = 1e5 +10 ;int h[N];int cnt; void down (int u) int t = u; if (2 * u <= cnt && h[2 * u] < h[t]) t = u * 2 ; if (2 * u + 1 <= cnt && h[2 * u + 1 ] < h[t]) t = u * 2 + 1 ; if (t != u) { swap (h[t], h[u]); down (t); } } int main () int n, m; cin >> n >> m; for (int i = 1 ; i <= n; ++ i) { cin >> h[i]; } cnt = n; for (int i = n / 2 ; i >= 1 ; -- i) down (i); int k = 1 ; while (m --) { printf ("%d " , h[1 ]); h[1 ] = h[cnt]; cnt --; down (1 ); } return 0 ; }
heap_swap()
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 #include <iostream> #include <cstring> const int N = 1e5 +10 ;int h[N], ph[N], hp[N];int cnt = 0 ;using namespace std;void heap_swap (int x, int y) swap (h[x], h[y]); swap (hp[x], hp[y]); swap (ph[hp[x]], ph[hp[y]]); } void down (int u) int t = u; if (2 * u <= cnt && h[2 * u] < h[t]) t = 2 * u; if (2 * u + 1 <= cnt && h[2 * u + 1 ] < h[t]) t = 2 * u + 1 ; if (t != u) { heap_swap (u, t); down (t); } } void up (int u) while (u / 2 && h[u / 2 ] > h[u]) { heap_swap (u, u / 2 ); u >>= 1 ; } } int main () int n; int pos = 0 ; cin >> n; while (n --) { char type[5 ]; scanf ("%s" , type); if (!strcmp (type,"I" )) { int num; scanf ("%d" , &num); pos ++; cnt ++; h[cnt] = num; hp[cnt] = pos; ph[pos] = cnt; up (cnt); } if (!strcmp (type, "PM" )) { int res; res = h[1 ]; cout << res << endl; } if (!strcmp (type,"DM" )) { heap_swap (1 , cnt); cnt --; down (1 ); } if (!strcmp (type, "D" )) { int pos, index; scanf ("%d" , &pos); index = ph[pos]; heap_swap (index, cnt); cnt --; up (index); down (index); } if (!strcmp (type, "C" )) { int k, x; scanf ("%d %d" , &k, &x); k = ph[k]; h[k] = x; up (k); down (k); } } return 0 ; }
问题描述:
如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。
例如,
[2,3,4] 的中位数是 3
[2,3] 的中位数是 (2 + 3) / 2 = 2.5
设计一个支持以下两种操作的数据结构:
void addNum(int num) - 从数据流中添加一个整数到数据结构中。
代码实现:
1、c++ stl中的优先队列
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 class MedianFinder {public : priority_queue<int , vector<int >, less<int >> maxHeap; priority_queue<int , vector<int >, greater<int >> minHeap; MedianFinder () { } void addNum (int num) if (maxHeap.size () == minHeap.size ()) { minHeap.push (num); int top = minHeap.top (); minHeap.pop (); maxHeap.push (top); } else { maxHeap.push (num); int top = maxHeap.top (); maxHeap.pop (); minHeap.push (top); } } double findMedian () if (maxHeap.size () == minHeap.size ()) { return (maxHeap.top ()+minHeap.top ())*1.0 /2 ; } else { return maxHeap.top ()*1.0 ; } } };
手动实现大根堆和小根堆
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 class MedianFinder {public : vector<int > minH; vector<int > maxH; int minCnt, maxCnt; void minDown (int u) int t = u; if (u*2 <= minCnt && minH[u*2 ] < minH[t]) t = u*2 ; if (u*2 +1 <= minCnt && minH[u*2 +1 ] < minH[t]) t = u*2 +1 ; if (u != t) { swap (minH[u], minH[t]); minDown (t); } } void minUp (int u) while (u / 2 && minH[u] < minH[u / 2 ]) { swap (minH[u], minH[u / 2 ]); u >>= 1 ; } } void maxDown (int u) int t = u; if (u*2 <= maxCnt && maxH[u*2 ] > maxH[t]) t = u*2 ; if (u*2 +1 <= maxCnt && maxH[u*2 +1 ] > maxH[t]) t = u*2 +1 ; if (u != t) { swap (maxH[u], maxH[t]); maxDown (t); } } void maxUp (int u) while (u / 2 && maxH[u] > maxH[u / 2 ]) { swap (maxH[u], maxH[u / 2 ]); u >>= 1 ; } } MedianFinder () { this ->maxH = vector <int >(1 , 0 ); this ->minH = vector <int >(1 , 0 ); minCnt = 0 ; maxCnt = 0 ; } void addNum (int num) if (maxCnt == minCnt) { maxCnt ++; maxH.push_back (num); maxUp (maxCnt); int tmp = maxH[1 ]; maxH[1 ] = maxH[maxCnt]; maxCnt --; maxDown (1 ); maxH.pop_back (); minCnt ++; minH.push_back (tmp); minUp (minCnt); } else { minCnt ++; minH.push_back (num); minUp (minCnt); int tmp = minH[1 ]; minH[1 ] = minH[minCnt]; minCnt --; minDown (1 ); minH.pop_back (); maxCnt ++; maxH.push_back (tmp); maxUp (maxCnt); } } double findMedian () if (minCnt == maxCnt) return (minH[1 ] + maxH[1 ]) / 2.0 ; else return 1.0 * minH[1 ]; } };
📔博文图谱
提及本博文的链接