区间DP

发表于 2022-05-22 更新于 2022-11-15 分类于 acwing算法基础课笔记 Artalk： loading...

区间DP

思路分析和相关例题

关于区间dp
区间类动态规划是线性动态规划的扩展，它在分阶段地划分问题时，与阶段中元素出现的顺序和由前一阶段的哪些元素合并而来有很大的关系。令状态 $f(i, j)$ 表示将下标位置 $i$ 到 $j$ 的所有元素合并能获得的价值的最大值，那么 $f(i,j)=max\{f(i,k)+f(k+1,j)+cost\},k\isin(i,j)$ ， $cost$ 为将这两组元素合并起来的代价。
@OI-Wiki区间DP

acwing 282. 石子合并

题目描述

解题思路

板书

状态表示 $f(i,j)$

集合: 所有将 $[i,j]$ 石子合并成一堆的方案的集合
属性: 方案的最小开销

$k$ 具有一般性，且 $k\isin(i,j)$

状态转移方程为 $f(i,j)=min_{k\isin(i,j)}\{f(i,k)+f(k+1,j)+cost\}$

其中 $cost$ 为 $i\sim j$ 的质量和，可用前缀和优化，即为 $s[j+1]$ - $s[i]$

代码实现

C++代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 310;

int n;
int s[N];
int f[N][N];

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &s[i]);

    for (int i = 1; i <= n; i ++ ) s[i] += s[i - 1];

    for (int len = 2; len <= n; len ++ )
        for (int i = 1; i + len - 1 <= n; i ++ )
        {
            int l = i, r = i + len - 1;
            f[l][r] = 1e8;
            for (int k = l; k < r; k ++ )
                f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
        }

    printf("%d\n", f[1][n]);
    return 0;
}

作者：yxc
链接：https://www.acwing.com/activity/content/code/content/58545/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

$Java$

import java.util.*;
import java.io.*;

class Main{
    static BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
    static final int N = 310;
    static final int INF =0x3f3f3f3f;
    public static void main(String[] args) throws Exception {
        int n = Integer.parseInt(cin.readLine().split(" ")[0]);
        String[] strs = cin.readLine().split(" ");
        int[] s = new int[N];
        for (int i = 1; i <= n; ++i) {
            s[i] = Integer.parseInt(strs[i - 1]);
            s[i] += s[i - 1];
        }
        int[][] dp = new int[N][N];
        // 先枚举长度
        for (int len = 2; len <= n; ++len) {
            for (int i = 1; i + len - 1 <= n; ++i) {
                int left = i, right = left + len - 1;
                dp[left][right] = INF;
                for (int k = left; k < right; ++k) {
                    dp[left][right] = Math.min(dp[left][right], dp[left][k] + dp[k + 1][right] + s[right] - s[left - 1]);
                }
            }
        }
        System.out.println(dp[1][n]);
        
        cin.close();
    }
}

面试题 08.14. 布尔运算

题目描述

给定一个布尔表达式和一个期望的布尔结果 result，布尔表达式由 0 (false)、1 (true)、& (AND)、 | (OR) 和 ^ (XOR) 符号组成。实现一个函数，算出有几种可使该表达式得出 result 值的括号方法。

示例

输入: s = "1^0|0|1", result = 0

输出: 2
解释: 两种可能的括号方法是
1^(0|(0|1))
1^((0|0)|1)

思路分析

表达式由真值（0、1）和布尔运算符构成，这里将问题拆分成子问题，用一个 $n\times n \times 2$ 维的数组存储中间结果

其中， $dp[i][j][0/1]$ 表示真值 $s[i]$ 到 $s[j]$ 之间的子表达式的运算结果为 $0$ 或 $1$ 的方案数量

针对每一个子问题：「求区间 $s[i,j]$ 构成的表达式的运算结果」，在区间 $[i,j]$ 上选取切分点，将子表达式分成左右两部分

根据真值表和乘法原理，将两部分（两个「子子」问题）的方案数相乘并累加进 $dp[i][j][]$

状态转移方程： $dp[i][j] = sum_{k\isin(i,j)}\{dp[i][k - 1] \times dp[k+1][j]\}$

真值表

$1$ 代表 true ， $0$ 代表 false

&与运算	1	0
1	1	0
0	0	0

｜或运算	1	0
1	1	1
0	1	0

^异或	1	0
1	0	1
0	1	0

代码实现

class Solution {
    public int countEval(String s, int result) {
        char[] chs = s.toCharArray();
        int n = chs.length;
        // 尝试区间DP做法
        int[][][] dp = new int[n][n][2];
        // 初始化，如果区间长度为 1 的话，运算结果就是元素本身的值
        for (int i = 0; i < n; ++i) {
            if (chs[i] == '0' || chs[i] == '1') {
                dp[i][i][chs[i] - '0'] = 1;
            }
        }
        // 区间DP，先枚举长度
        // 这里严谨点说，是「间隔」
        for (int len = 2; len <= n; len += 2) {
            // 再枚举左端点
            for (int i = 0; i < n - len + 1; i += 2) {
                int j = i + len; // 区间端点都是数字
                // 枚举切分点
                for (int k = i + 1; k <= j - 1; k += 2) {
                    if (chs[k] == '&') {
                        // 1 & 1 = 1
                        dp[i][j][1] += dp[i][k - 1][1] * dp[k + 1][j][1];
                        dp[i][j][0] += dp[i][k - 1][1] * dp[k + 1][j][0] + dp[i][k - 1][0] *  dp[k + 1][j][1] + dp[i][k - 1][0] * dp[k + 1][j][0];
                    }
                    if (chs[k] == '|') {
                        // 0 | 0 = 0
                        dp[i][j][0] += dp[i][k - 1][0] * dp[k + 1][j][0];
                        dp[i][j][1] += dp[i][k - 1][1] * dp[k + 1][j][0] + dp[i][k - 1][0] *  dp[k + 1][j][1] + dp[i][k - 1][1] * dp[k + 1][j][1];
                    }
                    if (chs[k] == '^') {
                        dp[i][j][1] += dp[i][k - 1][1] * dp[k + 1][j][0] + dp[i][k - 1][0] *  dp[k + 1][j][1];
                        dp[i][j][0] += dp[i][k - 1][1] * dp[k + 1][j][1] + dp[i][k - 1][0] *  dp[k + 1][j][0];
                    }
                }
            }
        }
        return dp[0][n - 1][result];
    }
}

其他思路

也可以采用分治的思路，枚举切分点，递归求出左右两部分的方案数量，再根据真值表和乘法原理处理结果。

可以借鉴记忆化搜索的思想，保存中间计算结果，用空间换时间。

代码

class Solution {
    public int countEval(String s, int result) {
        char[] chs = s.toCharArray();
        int n = chs.length;
        int[][][] cache = new int[n][n][];
        int[] res = dfs(chs, 0, n - 1, cache);
        return result == 0 ? res[0] : res[1];
    }
    // 记忆化搜索 + 分治
    public int[] dfs(char[] s, int left, int right, int[][][] cache) {
        // res[0] 代表 s[left-right] 运算结果为0的方案数量
        // res[1] 同理
        int[] res = new int[2];
        if (left >= right) {
            res[s[left] - '0'] = 1;
            return res;
        }
        // 如果命中缓存
        if (cache[left][right] != null) return cache[left][right];
        
        // 枚举切分点
        for (int i = left; i <= right; ++i) {
            if (s[i] == '0' || s[i] == '1') continue;
            int[] leftRes = dfs(s, left, i - 1, cache);
            int[] rightRes = dfs(s, i + 1, right, cache);
            // 下面根据真值表赋值
            if (s[i] == '&') {
                // 1 & 1 = 1 
                res[1] += leftRes[1] * rightRes[1];
                res[0] += leftRes[1] * rightRes[0] + leftRes[0] * rightRes[0] + leftRes[0] * rightRes[1];
            }
            if (s[i] == '|') {
                // 0 | 0 = 0
                res[0] += leftRes[0] * rightRes[0];
                res[1] += leftRes[1] * rightRes[0] + leftRes[1] * rightRes[1] + leftRes[0] * rightRes[1];
            }
            if (s[i] == '^') {
                // 0 ^ 1 = 1 and 1 ^ 0 = 1
                res[1] += leftRes[0] * rightRes[1] + leftRes[1] * rightRes[0];
                res[0] += leftRes[0] * rightRes[0] + leftRes[1] * rightRes[1];
            }
        }
        // 缓存结果
        cache[left][right] = res;
        return res;
    }
}

其他例题

1039. 多边形三角剖分的最低得分

题目描述

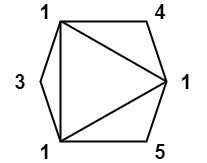
你有一个凸的 n 边形，其每个顶点都有一个整数值。给定一个整数数组 values ，其中 values[i] 是第 i 个顶点的值（即 顺时针顺序 ）。

假设将多边形剖分为 n - 2 个三角形。对于每个三角形，该三角形的值是顶点标记的乘积，三角剖分的分数是进行三角剖分后所有 n - 2 个三角形的值之和。

返回 多边形进行三角剖分后可以得到的最低分 。

示例

1
2
3

输入：values = [1,3,1,4,1,5]
输出：13
解释：最低分数三角剖分的得分情况为 1*1*3 + 1*1*4 + 1*1*5 + 1*1*1 = 13。

简要分析

多边形顶点依次编号为 1,2,3,...,n-1 ，记 $dp[i][j]$ 表示区间 $[i,j]$ 构成的多边形的 最低分

区间DP做法，先枚举区间长度 $len$ ，再枚举左侧起点 $i$ ，最后在当前区间内 $[i, i + len-1]$ ，枚举切割点 $k$

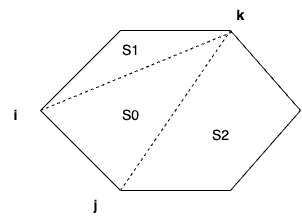
考虑一般情况如下图所示

leetcode1039.drawio

切割点 $k$ 将 $[i,j]$ 分成三个多边形，其中 $S_0$ 的得分为 values[i] * values[j] * values[k]

$S_1$ 的得分为 $dp[i][k]$ ， $S_2$ 的得分为 $dp[k][j]$ ，则区间的总得分为 $dp[i][k]+Score(S_0)+dp[k][j]$

枚举当前区间的所有的切割点，求出最小得分即可

代码实现

class Solution {
    static final int INF = 0x3f3f3f3f;
    public int minScoreTriangulation(int[] values) {
        int n = values.length;
        int[][] dp = new int[n][n]; 
        for (int len = 3; len <= n; ++len) { // 先枚举区间长度
            for (int i = 0; i < n - len + 1; ++i) {
                int l = i, r = i + len - 1;
                dp[l][r] = INF; // 求(l,r)区间的 最低分，先初始化为INF
                for (int k = l + 1; k < r; ++k) { // 枚举分割点
                    dp[l][r] = Math.min(dp[l][r], dp[l][k] + values[l] * values[r] * values[k] + dp[k][r]);
                }
            }
        }
        return dp[0][n - 1];
    }
}