快速排序和归并排序都是基于分治思想,平均时间复杂度都是 O ( n log 2 n ) \Omicron(n\log_2 n) O ( n log 2 n )
快排是不稳定 的,归并排序是稳定 的
快排的性能受初始数列的分布影响较大,最坏情况下时间复杂度达到 O ( n 2 ) \Omicron(n^2) O ( n 2 ) O ( n ) \Omicron(n) O ( n )
分治思想
确定分界点pivot
调整区间
暴力方法
一般方法—交换双指针
1 2 3 4 5 6 7 8 9 10 11 void quickSort (int q[], int l, int r) if (l >= r) return ; int x = q[l], i = l - 1 , j = r + 1 ; while (i < j){ do i++; while (q[i] < x); do j--; while (q[j] > x); if (i < j) swap (q[i], q[j]); } quickSort (q, l, j); quickSort (q, j + 1 , r); }
递归
代码1–yxc版本
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 #include <iostream> using namespace std;const int N = 1000010 ;int q[N];void quickSort (int q[], int l, int r) if (l >= r) return ; int x = q[l + r >> 1 ], i = l - 1 , j = r + 1 ; while (i < j){ do i++; while (q[i] < x); do j--; while (q[j] > x); if (i < j) swap (q[i], q[j]); } quickSort (q, l, j); quickSort (q, j + 1 , r); } int main () int n; scanf ("%d" , &n); for (int i = 0 ; i < n; ++i) scanf ("%d" , &q[i]); quickSort (q, 0 , n - 1 ); for (int j = 0 ; j < n; ++j) printf ("%d " , q[j]); return 0 ; }
代码2–严老师版本
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 #include <iostream> using namespace std;const int N = 1000010 ;int q[N];int helper (int q[], int low, int high) int pivot = q[low]; while (low < high) { while (low < high && q[high] >= pivot) --high; q[low] = q[high]; while (low < high && q[low] <= pivot) ++low; q[high] = q[low]; } q[low] = pivot; return low; } void quickSort (int q[], int l, int r) if (l < r) { int pivotPos = helper (q, l, r); quickSort (q, l, pivotPos - 1 ); quickSort (q, pivotPos + 1 , r); } } int main () int n; scanf ("%d" , &n); for (int i = 0 ; i < n; ++i) scanf ("%d" , &q[i]); quickSort (q, 0 , n - 1 ); for (int j = 0 ; j < n; ++j) printf ("%d " , q[j]); return 0 ; }
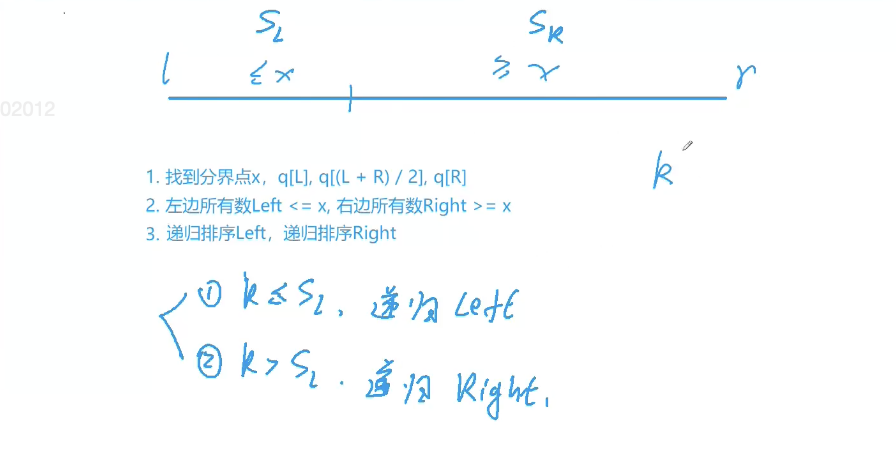
acwing 786. 第k个数
与快排不同,每次迭代,只需递归一边。
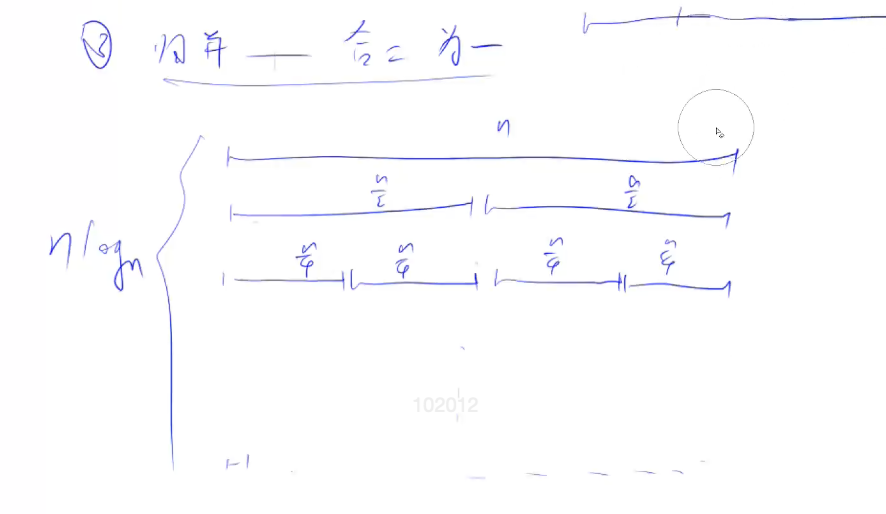
复杂度O ( n ) \Omicron(n) O ( n )
第一次迭代 n n n 第二次迭代 n 2 \frac{n}{2} 2 n …… n + n 2 + n 4 + n 8 + ⋯ = n ( 1 + 1 2 + 1 4 + 1 8 + ⋯ ) n+\frac{n}{2}+\frac{n}{4}+\frac{n}{8}+\cdots=n(1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\cdots) n + 2 n + 4 n + 8 n + ⋯ = n ( 1 + 2 1 + 4 1 + 8 1 + ⋯ ) 而lim n → ∞ 1 + 1 2 + 1 4 + 1 8 + ⋯ + 1 2 n = 2 \lim_{n\to\infty}1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\cdots+\frac{1}{2^{n}}=2 lim n → ∞ 1 + 2 1 + 4 1 + 8 1 + ⋯ + 2 n 1 = 2 所以是O ( n ) \Omicron(n) O ( n ) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 #include <iostream> using namespace std;const int N = 1000010 ;int q[N];int n, k;int quickSelect (int l, int r, int k) if (l == r) return q[l]; int x = q[l]; int i = l - 1 , j = r + 1 ; while (i < j){ while (q[++i] < x); while (q[--j] > x); if (i < j) swap (q[i], q[j]); } int sl = j - l + 1 ; if (k <= sl) return quickSelect (l, j, k); return quickSelect (j + 1 , r, k - sl); } int main () cin >> n >> k; for (int i = 0 ; i < n; ++i){ cin >> q[i]; } cout << quickSelect (0 , n - 1 , k) << endl; return 0 ;
注意事项 :背诵模板的目的之一在于边界情况的处理 ,避免重复思考。
分治思想
归并排序是稳定 的
采用递归实现,本质是先将数组二分切成一个个小数组,直到每个小数组长度为1(因为只有一个元素时,数组一定有序),再逐步合并新的有序序列,以此递推。
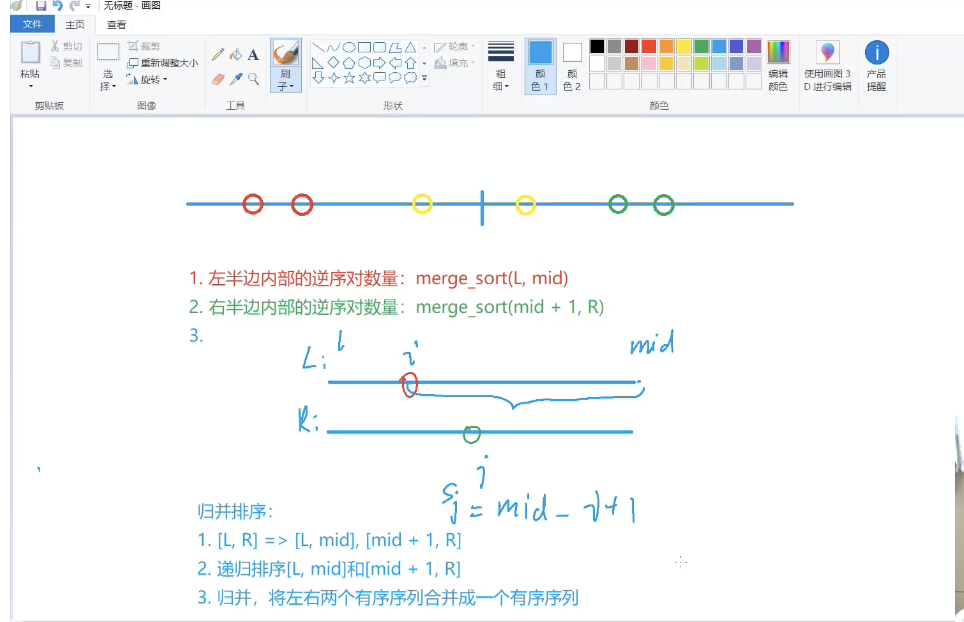
代码流程:
确定分界点 mid=(left+right)/2;
递归排序左右两部分
“归并”——合二为一
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 #include <iostream> using namespace std;const int N = 1000010 ;int n;int q[N], tmp[N];void mergeSort (int q[], int l, int r) if (l >= r) return ; int mid = l + r >> 1 ; mergeSort (q, l, mid); mergeSort (q, mid + 1 , r); int k = 0 ,i = l, j = mid + 1 ; while (i <= mid && j <= r){ if (q[i] <= q[j]) tmp[k++] = q[i++]; else tmp[k++] = q[j++]; } while (i <= mid) tmp[k++] = q[i++]; while (j <= r) tmp[k++] = q[j++]; for (i = l, j = 0 ; i <= r; ++i, j++) q[i] = tmp[j]; } int main () scanf ("%d" , &n); for (int i = 0 ; i < n; ++i) scanf ("%d" , &q[i]); mergeSort (q, 0 , n - 1 ); for (int i = 0 ; i < n; ++i) printf ("%d" , q[i]); }
算法时间复杂度: O ( n log 2 n ) \Omicron(n\log_2n) O ( n log 2 n )
@2022年 3月24日 星期四 23时15分27秒 CST
更新自底向上 的写法
参考自顶向下归并排序和自底向上的归并排序
自底向上可以采用循环实现。开始,直接将数组两两归并,此轮循环后,数组变成两两有序的;然后每四个归并,数组变成每四个是有序的 … \dots … ⌊ 2 x ⌋ = n \lfloor{2^{x}}\rfloor=n ⌊ 2 x ⌋ = n x x x
J a v a Java J a v a
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 public int [] mergeSort(int [] nums) { int n = nums.length; int [] tmp = new int [n]; int start, mid, end, i, j, k; for (int len = 1 ; len < n; len = 2 * len) { for (start = 0 ; start < n; start = start + 2 * len) { mid = start + len - 1 ; end = Math.min(start + 2 * len - 1 , n - 1 ); if (mid > end) mid = start + end >> 1 ; i = start; j = mid + 1 ; k = 0 ; while (i <= mid && j <= end) { if (nums[i] <= nums[j]) tmp[k++] = nums[i++]; else tmp[k++] = nums[j++]; } while (i <= mid) tmp[k++] = nums[i++]; while (j <= end) tmp[k++] = nums[j++]; for (i = start, j = 0 ; i <= end; ++i, ++j) nums[i] = tmp[j]; } } return nums; }
代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 #include <iostream> using namespace std;typedef long long LL;const int N = 100010 ;int q[N], tmp[N];LL mergeSort (int l, int r) { if (l >= r) return 0 ; int mid = l + r >> 1 ; LL res = mergeSort (l, mid) + mergeSort (mid + 1 , r); int k = 0 , i = l, j = mid + 1 ; while (i <= mid && j <= r){ if (q[i] <= q[j]) tmp[k++] = q[i++]; else { tmp[k++] = q[j++]; res += mid - i + 1 ; } } while (i <= mid) tmp[k++] = q[i++]; while (j <= r) tmp[k++] = q[j++]; for (i = l, j = 0 ; i <= r; ++i, ++j){ q[i] = tmp[j]; } return res; } int main (void ) int n; cin >> n; for (int i = 0 ; i < n; ++i){ cin >> q[i]; } cout << mergeSort (0 , n - 1 ) << endl; return 0 ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 class Solution { public ListNode mergeKLists (ListNode[] lists) { int len = lists.length; if (len == 0 || len == 1 && lists[0 ] == null ) return null ; return merge(lists, 0 , len - 1 ); } ListNode merge (ListNode[] lists, int l, int r) { if (l > r) return null ; if (l == r) return lists[l]; int mid = l + r >> 1 ; ListNode left = merge(lists, l, mid); ListNode right = merge(lists, mid + 1 , r); return mergeListNode(left, right); } ListNode mergeListNode (ListNode x, ListNode y) { ListNode res = new ListNode (0 ); ListNode p = res; while (x != null && y != null ) { if (x.val < y.val) { p.next = x; x = x.next; } else { p.next = y; y = y.next; } p = p.next; } if (x != null ) p.next = x; if (y != null ) p.next = y; return res.next; } }
Tips
找链表的中点,可以用快慢指针的方法,快指针每次移动2步,慢指针每次移动1步,当快指针到达链表末尾时,慢指针指向的链表节点即为链表的中点。
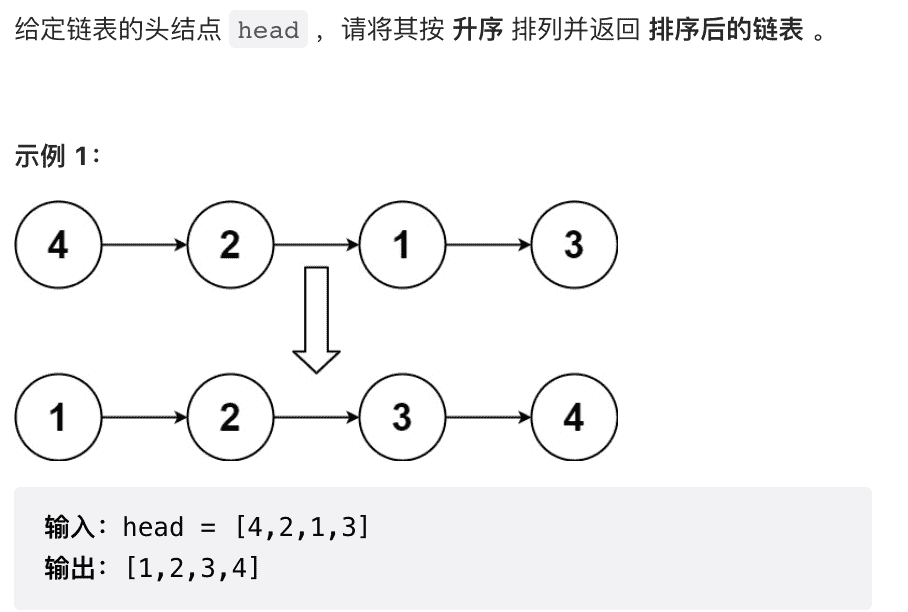
要求:在 O ( n log n ) \Omicron(n\log{n}) O ( n log n ) O ( 1 ) \Omicron(1) O ( 1 )
链表排序–>不能随机访问–>快排和堆排不能用–>只能用归并排序
基于分治的思想
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 class Solution { public ListNode sortList (ListNode head) { return merge(head); } ListNode merge (ListNode list) { if (list == null ) return null ; if (list.next == null ) return list; ListNode midNode = findMid(list); ListNode rightStart = midNode.next; midNode.next = null ; ListNode left = merge(list); ListNode right = merge(rightStart); return mergeListNode(left, right); } ListNode mergeListNode (ListNode x, ListNode y) { ListNode res = new ListNode (0 ); ListNode p = res; while (x != null && y != null ) { if (x.val < y.val) { p.next = x; x = x.next; } else { p.next = y; y = y.next; } p = p.next; } if (x != null ) p.next = x; if (y != null ) p.next = y; return res.next; } ListNode findMid (ListNode head) { ListNode dummy = new ListNode (0 , head); ListNode fast = dummy, slow = dummy; while (fast != null && fast.next != null ) { fast = fast.next.next; slow = slow.next; } return slow; } }
注意细节:
1 2 ListNode rightStart = midNode.next;midNode.next = null ;
不要忘记将链表截断,分成两个独立的链表,否则会产生死循环。
📔博文图谱
提及本博文的链接