个人认为,Manacher算法和Kmp 有异曲同工之妙
之前转载过一篇关于Manacher算法的乐扣题解 。初次学习,不甚理解,最近复习了Kmp算法后,豁然开朗
LeetCode 5. 最长回文子串
给出一个字符串 s ,找到 s 中的最长回文子串
子串:不可以删减个别字符,区别于「子序列」,连续子序列
回文串:正向和反向输出一致的字符串。例如:“明天到操场操到天明”
示例
1 2 input: s = "abac" output: "aba"
最直观的做法,枚举每个子串,然后判断各自是否为回文串
1 2 3 4 5 6 7 8 9 10 11 for (int i = 1 ; i < n; ++i) { for (int j = i; j >= 0 ; --j) { if (isPalind(s, j, i)) { if (res < end - start) { start = j; end = i + 1 ; } } } } return s.substring(start, end);
枚举每个子串的时间复杂度是 O ( n 2 ) \Omicron(n^2) O ( n 2 ) O ( n ) \Omicron(n) O ( n )
整体下来的时间复杂度为 O ( n 3 ) \Omicron(n^3) O ( n 3 )
由于回文串是「中心对称」的,判断回文串一般也是利用两个指针,从两边向中间扫描,进行比较
降低时间复杂度,我们可以减少指针扫描的躺数,将枚举子串和判断回文串结合起来
具体做法是,最外层循环,将每次枚举的点作为回文中心,然后用两个指针l和r向外拓展,如果 s[l] != s[r] ,即可终止扫描。不是回文串的子串是没有必要枚举的。
这就是中心拓展,时间复杂度降低到 O ( n 2 ) \Omicron(n^2) O ( n 2 )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 for (int i = 0 ; i < n; ++i) { int cur = Math.max(maxP(s, i, i), maxP(s, i, i + 1 )); if (cur > end - start + 1 ) { start = i - (cur - 1 ) / 2 ; end = i + cur / 2 ; } } public int maxP (String s, int l, int r) { int n = s.length(); while (l >= 0 && r < n && s.charAt(l) == s.charAt(r)) { l--; r++; } return r - l - 1 ; }
中心拓展算法之所以是 O ( n 2 ) \Omicron(n^2) O ( n 2 )
Manacher算法是在中心拓展的基础上进行了优化,针对每个回文中心,会利用已有的信息,生成一个初始拓展距离,并不会从零开始
重点在于,何为『已有的信息?』,下面举例说明
令 f [ i ] f[i] f [ i ] s [ i ] s[i] s [ i ]
核心是利用了「回文串的对称性」
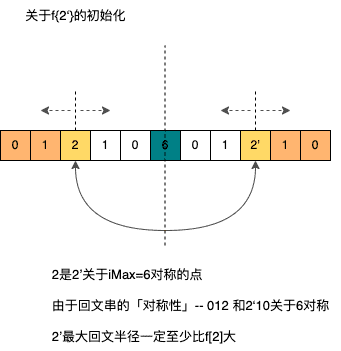
例如,一个字符串s="012106 01210"是个回文串,"01210"和"012 ’10"关于‘6’对称,当扫描到2 ’时,由于已知s是回文串,那么2 ’关于2对称,2 ’两侧的字符串也同样地和2两侧的字符串对称,那么
「2 ’目前 可以拓展的距离必定和2相同」
由于以2为中心的最大回文半径f[2]已经记录下来,因此f{2 ’}可以直接初始化 为f[2],而不必从零开始拓展
利用数组 f [ ] f[] f [ ]
在枚举每个回文中心的迭代中,维持两个变量:
iMax。子串 s [ 0 → i ] s[0\to i] s [ 0 → i ] rMax。 s [ 0 → i ] s[0 \to i] s [ 0 → i ] iMax + f [ iMax ] − 1 \text{iMax} + f[\text{iMax}] - 1 iMax + f [ iMax ] − 1 迭代枚举回文中心 i i i
初始化 f [ i ] f[i] f [ i ] j = 2 × i M a x − i j=2\times iMax - i j = 2 × i M a x − i i i i i M a x iMax i M a x 如果 i < r M a x i < rMax i < r M a x i i i i M a x iMax i M a x j j j f [ j ] f[j] f [ j ] f [ i ] f[i] f [ i ] i M a x iMax i M a x f [ i ] = m i n { f [ j ] , r M a x − i + 1 } f[i] = min\{f[j], rMax-i + 1\} f [ i ] = m i n { f [ j ] , r M a x − i + 1 } 如果 i > r M a x i > rMax i > r M a x i i i i M a x iMax i M a x f [ ] f[] f [ ] f [ i ] = 1 f[i]=1 f [ i ] = 1 在初始化的基础上,开始向两边拓展 在迭代中,如果以当前 i i i r M a x − i M a x + 1 rMax-iMax + 1 r M a x − i M a x + 1 i M a x iMax i M a x r M a x rMax r M a x
Kmp算法,利用了next数组,在失配时,主串不用后退,而是利用已知的「相等前后缀」信息,移动副串即可
Manacher算法类似,利用回文串的对称性,利用已知的对称点的最大半径信息,来初始化该点的 f [ i ] f[i] f [ i ] r M a x rMax r M a x O ( n ) \Omicron(n) O ( n )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 public String longestPalindrome (String s) { if (s == null || s.length() < 1 ) { return "" ; } int rm = 0 , im = 0 , n = s.length(); StringBuilder sb = new StringBuilder (); sb.append("$#" ); for (int i = 0 ; i < n; ++i) { char ch = s.charAt(i); sb.append(ch); sb.append('#' ); } sb.append('!' ); char [] chs = sb.toString().toCharArray(); int m = chs.length; int [] f = new int [m - 1 ]; int start = 0 , end = 0 ; for (int i = 1 ; i < m - 1 ; ++i) { f[i] = (i <= rm) ? Math.min(rm - i + 1 , f[2 * im - i]) : 1 ; while (chs[i + f[i]] == chs[i - f[i]]) ++f[i]; if (f[i] > rm - im + 1 ) { im = i; rm = i + f[i] - 1 ; start = i - f[i] + 1 ; end = i + f[i] - 1 ; } } StringBuilder res = new StringBuilder (); for (int i = start; i <= end; ++i) { if (chs[i] == '#' ) continue ; res.append(chs[i]); } return res.toString(); }
📔博文图谱
提及本博文的链接