向阳花

Tips

字符串处理

leetcode 2047.句中的有效单词数

2047. 句子中的有效单词数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
public:
    bool check(string s) {
        int k = 0;
        // 若有多个空格 快速返回结果
        if (s.size() == 0) return false;
        for (int i = 0; i < s.size(); ++ i) {
            // 处理标点符号
            if (s[i] == '!' || s[i] == '.' || s[i] == ',') {
                if (i != s.size() - 1) return false;
            }
            // 处理数字
            if (isdigit(s[i])) return false;
            if (s[i] == '-') {
                // 最多一个连字符
                if (k ++) return false;
                // '||' 运算符有夹断作用
                if (i == 0 || i == s.size() - 1 || !isalpha(s[i + 1])) return false;
            }
        }
        return true;
    }
    int countValidWords(string sentence) {
        string tmp = "";
        int cnt = 0;
        for (int i = 0; i < sentence.size(); ++ i) {
            if (sentence[i] == ' ') {
                if (check(tmp)) cnt ++;
                tmp = "";
                continue;
            }
            tmp += sentence[i];
        }
        // 处理最后一个token后没有空格的情况
        if (check(tmp)) cnt ++;
        return cnt;
    }
};

acwing 3302.表达式求值

关于字符串处理部分
获得一个字符串中连续的数字

1
2
3
4
5
6
7
8
9
10
11
12
13
// stack<int> num;
for (int i = 0; i < str.size(); ++ i) {
        char ch = str[i];
        if (isdigit(ch)) {
            int x = 0, j = i;
            while (j < str.size() && isdigit(str[j])) {
                x = x * 10 + (str[j ++] - '0');
            }
            i = j - 1;
            num.push(x);
        }
    }

8. 字符串转换整数 (atoi)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    int myAtoi(string s) {
        int sign = 1;
        int i = 0;
        // 丢弃无用的空格
        for (; i < s.size(); ++ i) {
            if (s[i] != ' ') break;
        }
        if (s[i] == '-') sign = -1; 
        // 用来判断类似"  .123"这样的case，首有效字符非正负号也非数字，直接返回0
        if (!isdigit(s[i]) && s[i] != '-' && s[i] != '+') return 0;
        int ans = 0;
        int start = i;
        for (int i = start; i < s.size(); ++ i) {
            if (i > start && !isdigit(s[i])) break; // 数字字符部分结束
            if (i == start && !isdigit(s[i])) continue; // 跳过正负符号位
            if ((INT_MAX - (s[i] - '0')) / 10 < ans) { // 判断加上当前数位后,是否会超出INT_MAX
                // 若超出，直接返回INT_MAX 或者INT_MIN
                if (sign == 1) return INT_MAX;
                else return INT_MIN;
            }
            ans = ans * 10 + (s[i] - '0');
        }
        return ans * sign;
    }
};

Java-leetcode-Tips

需要对字符串修改时

  1. 可以先转化为字符数组进行处理，最后再转换回来。

    • cs = str.toCharArray();
    • String res = String.valueOf(cs);

  2. 使用StringBuilder

    • StringBuilder sb = new StringBuilder(str);
    • sb.setCharAt(i, 'ch');

List转化为二维数组

1
2
List<int[]> res = new ArrayList<>();
int[][] resArr = res.toArray(new int[res.size()][]);

排序-自定义构造器

java

例如：

1
2
3
4
5
6
7
8
9
class Pair{
    private int index;
    private int freq;
    
    public Pair(int freq, char ch) {
            this.freq = freq;
            this.ch = ch;
    }
}

需求：按照Pair的freq属性从大到小排序。

1
2
3
4
5
6
7
8
9
List<Pair> arr = new ArrayList<>();
// Lambda表达式
Arrays.sort(arr, (p1, p2) -> p2.freq - p1.freq);
// 重写比较器的compare方法
Arrays.sort(arr, new Comparator<Pair>() {
    public int compare(Pair a, Pair b) {
        return b.freq - a.freq;
    }
});

C++

1
2
3
sort(arr.begin(), arr.end(), [](const pair<int, char> & p1, const pair<int, char> & p2) {
    return p1.first > p2.first;
});

Ps:

如何快速对int数组排序？

例如：剑指 Offer II 074. 合并区间中需要按照intervals[i][0]的大小顺序对二维数组intervals[][]进行排序

Sol1:

自己手写快排

1
2
3
4
5
6
7
8
9
10
11
12
13
void quickSort(int[][] q, int l, int r) {
    if (l >= r) return;
    int x = q[l + r >> 1][0], i = l - 1, j = r + 1;
    while (i < j) {
        while (q[++i][0] < x);
        while (q[--j][0] > x);
        if (i < j) {
            int[] tmp = q[i]; q[i] = q[j]; q[j] = tmp;
        }
    }
    quickSort(q, l, j);
    quickSort(q, j + 1, r);
}
Sol2:

先将 intint 数组装箱，然后再写 LambdaLambda 表达式，最后再转移回来

1
nums = Arrays.stream(nums).boxed().sorted((a, b) -> b - a).mapToInt(p -> p).toArray();

C++自定义哈希函数

c++ 不能直接将pair类型的变量放入集合或者哈希表，需要自己提供一个哈希函数

1
2
3
4
5
auto hash_p = [](const pair<int, int> &p) -> size_t {
    static hash<long long> hash_ll;
    return hash_ll(p.first + (static_cast<long long>(p.second) << 32));
};
unordered_set<pair<int, int>, decltype(hash_p)> points(0, hash_p);

回溯问题

学习自代码随想录的力扣题解

代码随想录-回溯法理论

  1. 确定递归的返回条件
  2. 确定是组合问题还是排列问题
    • 元素是否可以重复利用
    • 确定函数的参数列表
  3. 确定每个树层的搜索逻辑

脑子里要有个清晰的递归树，树层，树枝，是在代码的何处进入和出去的。

47.全排列 II

经典回溯问题

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

输入：nums=[1,1,2]

输出：[[1,1,2],[1,2,1],[2,1,1]]

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public List<List<Integer>> permuteUnique(int[] nums) {
        Arrays.sort(nums); // 排序
        List<List<Integer>> res = new ArrayList<>();
        List<Integer> cur = new ArrayList<>();
        boolean[] used = new boolean[nums.length];
        dfs(res, cur, nums, used);
        return res;
    }
    void dfs(List<List<Integer>> res, List<Integer> cur, int[] q, boolean[] used) {
        if (cur.size() == q.length) {
            res.add(new ArrayList<>(cur));
            return;
        }
        for (int i = 0; i < q.length; ++i) {
            if (i > 0 && q[i] == q[i - 1] && used[i - 1] == false) continue; // 树层剪枝，通过排序，相等的数字一定挨着
            if (used[i] == true) continue; // 树枝剪枝，用过的数字不能再用
            cur.add(q[i]);
            used[i] = true;
            dfs(res, cur, q, used);
            used[i] = false;
            cur.remove(cur.size() - 1);
        }
    }
}

二叉树的前/中/后遍历——迭代版本

144. 二叉树的前序遍历

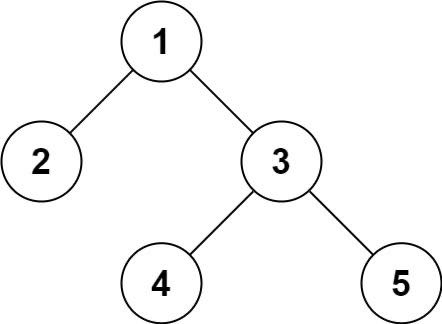
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        if (root == nullptr) return {};
        stack<TreeNode*> st;
        vector<int> res;
        st.push(root);
        while (!st.empty()) {
            TreeNode* p = st.top();
            st.pop();
            res.push_back(p->val);
            if (p->right != nullptr) st.push(p->right);
            if (p->left != nullptr) st.push(p->left);
        }
        return res;
    }
};

94. 二叉树的中序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        if (root == nullptr) return {};
        vector<int> ans;
        stack<TreeNode*> s;
        TreeNode* curr = root;
        while (curr != nullptr || !s.empty()) {
            // 每次遍历到最左边节点 
            // 中序遍历的特点
            while (curr != nullptr) {
                s.push(curr);
                curr = curr->left;
            }
            //
            curr = s.top(); s.pop();
            ans.push_back(curr->val);
            //
            curr = curr->right;
        }    
        return ans;
    }
};

145. 二叉树的后序遍历

反转前序遍历

c++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        // reverse_postorder
        // 最后再翻转一下结果
        if (!root) return {};
        deque<int> ans;
        stack<TreeNode*> s;
        s.push(root);
        while (!s.empty()) {
            TreeNode* n = s.top();
            s.pop();
            // reverse(print(root), right(), left());
            // 根-右-左 的访问顺序，最后一反转，就是后序遍历的顺序
            // 这里利用双端队列deque，每次将出栈节点的值放入队首，省去了reverse的步骤
            ans.push_front(n->val); // O(1)
            // 因为栈是先进后出，所以要想先访问右节点，先将左节点入栈
            if (n->left) s.push(n->left);
            if (n->right) s.push(n->right);
        }   
        return vector<int>(ans.begin(), ans.end());
        
    }
};

java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if (root == null) return res;
        // 反转前序遍历 NRL --reverse--> LRN后序遍历
        Deque<TreeNode> st = new ArrayDeque<>();
        st.push(root);
        while (!st.isEmpty()) {
            TreeNode cur = st.peek();
            res.add(st.pop().val);
            if (cur.left != null) st.push(cur.left);
            if (cur.right != null) st.push(cur.right);
        }
         Collections.reverse(res);
        return res;
    }
}
迭代版本

c++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    vector<int> postorderTraversal(TreeNode *root) {
        if (!root) return {};
        vector<int> vec;
        stack<TreeNode *> stk;
        TreeNode *prev = nullptr;
        auto node = root;
        while (!stk.empty() || node) {
            // 1.遍历到最左子节点
            while (node) {
                stk.push(node);
                node = node->left;
            }
            node = stk.top(); stk.pop();
            // 2.遍历最左子节点的右子树(右子树存在 && 未访问过)
            if (node->right && node->right != prev) {
                // 重复压栈以记录当前路径分叉节点
                stk.push(node);
                node = node->right;      
            } else {
                // 后序：填充vec在node->left和node->right后面
                // 注意：此时node的左右子树应均已完成访问
                vec.push_back(node->val);
                // 避免重复访问右子树[记录当前节点便于下一步对比]
                prev = node;
                // 避免重复访问左子树[设空节点]
                node = nullptr;
            }
        }
        return vec;
    }
};
迭代优化版本

java

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if (root == null) return res;
        
        Deque<TreeNode> st = new ArrayDeque<>();
        //
        Set<TreeNode> v = new HashSet<>();
        st.push(root);
        while (!st.isEmpty()) {
            TreeNode cur = st.peek();

            if ((cur.right == null && cur.left == null) || v.contains(cur)) {
                st.pop();
                res.add(cur.val);
                continue;
            }
            if (cur.right != null) st.push(cur.right);
            if (cur.left != null) st.push(cur.left);
            v.add(cur);
        }
        return res;
    }
}
拓展：590. N 叉树的后序遍历

102. 二叉树的层序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> q;
        vector<vector<int>> res;
        if (root == nullptr) return res;
        //
        q.push(root);
        while (!q.empty()) {
            int size = q.size();
            vector<int> tmp;
            while (size --){
                TreeNode *cur = q.front(); q.pop();
                tmp.push_back(cur->val);
                if (cur->left != nullptr) q.push(cur->left);
                if (cur->right != nullptr) q.push(cur->right);
            }
            res.push_back(tmp);
        }
        return res;
    }
};
层序遍历–BFS相关例题
剑指 Offer 32 - I. 从上到下打印二叉树

从上到下打印出二叉树的每个节点，同一层的节点按照从左到右的顺序打印。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    vector<int> levelOrder(TreeNode* root) {
        vector<int> res;
        queue<TreeNode*> q;
        if (root == NULL) return res;
        q.push(root);
        while (!q.empty()) {
            int n = q.size();
            while (n --) {
                TreeNode *tmp = q.front(); q.pop();
                res.emplace_back(tmp->val);
                if (tmp->left != NULL) q.push(tmp->left);
                if (tmp->right != NULL) q.push(tmp->right); 
            }
        }
        return res;
    }
};
剑指 Offer 32 - II. 从上到下打印二叉树 II

从上到下按层打印二叉树，同一层的节点按从左到右的顺序打印，每一层打印到一行。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> res;
        if (root == NULL) return res;
        queue<TreeNode*> q;
        q.push(root);
        
        while (!q.empty()) {
            vector<int> temp;
            for (int i = q.size(); i > 0; -- i) {
                TreeNode *tmp = q.front();
                q.pop();
                temp.push_back(tmp->val);
                if (tmp->left != NULL) q.push(tmp->left);
                if (tmp->right != NULL) q.push(tmp->right);
            }
            res.push_back(temp);
        }
        return res;
    }
};
剑指 Offer 32 - III. 从上到下打印二叉树 III

请实现一个函数按照之字形顺序打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右到左的顺序打印，第三行再按照从左到右的顺序打印，其他行以此类推。

引入双端队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> res;
        if (root == NULL) return res;
        // 双端队列
        // 可得好好复习 双端队列的问题！！！
        deque<TreeNode*> dq;
        dq.push_back(root);
        // 代表层数
        int flag = 0;
        while (!dq.empty()) {
            vector<int> tmpAns;
            int n = dq.size();
            while (n --) {
                TreeNode *cur;
                // 奇数层
                if (flag & 1) {
                    cur = dq.back();
                    dq.pop_back();
                    tmpAns.push_back(cur->val);
                    if (cur->right != NULL) dq.push_front(cur->right);
                    if (cur->left != NULL) dq.push_front(cur->left);
                }
                else {
                    cur = dq.front();
                    dq.pop_front();
                    tmpAns.push_back(cur->val);
                    if (cur->left != NULL) dq.push_back(cur->left);
                    if (cur->right != NULL) dq.push_back(cur->right);
                }
            }
            res.push_back(tmpAns);  
            flag ++;     
        }
        return res;
    }
};

Morris遍历-空间占用O(1)

参考 神级遍历——morris

Morris中序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public List<Integer> inorderTraversal(TreeNode root) {
    List<Integer> res = new ArrayList<>();
    // Morris遍历
    // 利用空指针存储，链接信息，指针回退
    TreeNode cur = root;
    TreeNode rightmost = null;
    while (cur != null) {
        rightmost = cur.left;
        if (cur.left != null) {
            // 找到当前节点cur 的左子树的 最右节点
            while (rightmost.right != null && rightmost.right != cur) {
                rightmost = rightmost.right;
            }
            // 建立指向cur的右指针，方便后退回去
            // 相当于把存在栈中的指针用空闲的右指针存了
            if (rightmost.right == null) {
                rightmost.right = cur;
                cur = cur.left;
                continue;
            } else rightmost.right = null; // 切断联系，释放掉之前占用的右指针
        }
        res.add(cur.val);
        cur = cur.right;
    }
    return res;
}

Morris先序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public List<Integer> preorderTraversal(TreeNode root) {
    List<Integer> res = new ArrayList<>();
    // Morris 遍历
    TreeNode cur = root;
    TreeNode mostright = null;
    while (cur != null) {
        mostright = cur.left;
        if (mostright != null) {
            while (mostright.right != null && mostright.right != cur) mostright = mostright.right;
            if (mostright.right == null) {
                mostright.right = cur;
                res.add(cur.val);
                cur = cur.left;
                continue;
            } else mostright.right = null;
        } else res.add(cur.val);
        cur = cur.right;
    }
    return res;
}

二叉树的序列化相关问题

序列化二叉树

实现LeetCode上序列化二叉树的方式

例如

RY3s5M-2

1
2
输入：root = [1,2,3,null,null,4,5]
输出：[1,2,3,null,null,4,5]

序列化

层序遍历的思路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
    if (root == null) return "[]";
    StringBuffer sb = new StringBuffer("[");
    Queue<TreeNode> q = new LinkedList<>();
    q.offer(root);
    while (!q.isEmpty()) {
        TreeNode cur = q.poll();
        if (cur != null) {
            sb.append(cur.val + ",");
            q.offer(cur.left);
            q.offer(cur.right);
        } else sb.append("null,");
    }
    sb.deleteCharAt(sb.length() - 1);
    sb.append("]");
    return sb.toString();
}

反序列化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
    if (data.equals("[]")) return null;
    String[] arr = data.substring(1, data.length() - 1).split(",");
    TreeNode root = new TreeNode(Integer.parseInt(arr[0]));
    Queue<TreeNode> q = new LinkedList<>();
    q.offer(root);
    int idx = 1;
    while (!q.isEmpty()) {
        TreeNode curNode = q.poll();
        if (!"null".equals(arr[idx])) {
            curNode.left = new TreeNode(Integer.parseInt(arr[idx]));
            q.offer(curNode.left);
        } 
        idx++;
        if (!"null".equals(arr[idx])) {
            curNode.right = new TreeNode(Integer.parseInt(arr[idx]));
            q.offer(curNode.right);
        }      
        idx++;
    }
    return root;
}

从中序和前序遍历序列构建二叉树

leetcode: 105. 从前序与中序遍历序列构造二叉树

给出前序遍历和中序遍历的序列，构建二叉树

ps：indexMap保存节点值到中序遍历序列中索引的映射，用于快速定位中序遍历序列中根节点的位置

节点值必须无重复

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public Map<Integer, Integer> indexMap;
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        int n = preorder.length;
        indexMap = new HashMap<>();
        for (int i = 0; i < inorder.length; ++i) {
            indexMap.put(inorder[i], i);
        }
        return build(preorder, inorder, 0, n - 1, 0, n - 1);
    }

    public TreeNode build(int[] preorder, int[] inorder, int preLeft, int preRight, int inLeft, int inRight) {
        if (preLeft > preRight) return null; // null
        TreeNode root = new TreeNode(preorder[preLeft]);
        int inorderRootIdx = indexMap.get(preorder[preLeft]); // 中序遍历序列中，根节点的索引
        int numsOfLeft = inorderRootIdx - inLeft; // 左子树的节点个数
        // 递归构建左子树
        root.left = build(preorder, inorder, preLeft + 1, preLeft + numsOfLeft, inLeft, inorderRootIdx - 1);
        // 递归构建右子树
        root.right = build(preorder, inorder, preLeft + numsOfLeft + 1, preRight, inorderRootIdx + 1, inRight);
        return root;
    }
}

前序遍历：Root node,[Left subtree的前序],[Right subtree的前序]

中序遍历：[Left subtree的中序],Root node,[Right subtree的中序]

二叉树的路径问题

参见星晴Pro的乐扣题解

剑指 Offer 55 - II. 平衡二叉树–经典dfs

输入一棵二叉树的根节点，判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1，那么它就是一棵平衡二叉树。

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    bool isBalanced(TreeNode* root) {
        if (root == NULL) return true;
        int left = depth(root->left);
        int right = depth(root->right);
        return abs(right - left) <= 1 && isBalanced(root->left) && isBalanced(root->right);
    }
    int depth(TreeNode *root) {
        if (root == NULL) return 0;
        return max(depth(root->left), depth(root->right)) + 1;
    }
};

图论——建图&搜索

建图

邻接表法

为节点A添加一条指向节点B的边

A节点的值为a，B节点同理

1
2
3
4
5
void add(int a, int b) {
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

DFS-深度优先遍历

1
2
3
4
5
6
7
8
9
void dfs(int u) {
    visited[u] = true;
    for (int i = h[u]; i != -1; i = ne[i]) {
        int val = e[i];
        if (!visited[val]) {
            dfs(val);
        }
    }
}

BFS-广度优先遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void bfs(int u) {
    Queue<Integer> q = new LinkedList<>();
    q.offer(u);
    while (!q.isEmpty()) {
        int size = q.size();
        while (size-- > 0) {
            int cur = q.poll();
            for (int i = h[cur]; i != -1; i = ne[i]) {
                int val = e[i];
                if (!visited[val]) {
                    q.offer(val);
                    visited[val] = true;
                }
            }
        }
    }
}

几处细节

  1. 首先，关于各个数组的含义

以下默认节点序号即为节点的值，例如

treeNode.drawio

h[N]，数组的索引为：节点序号，数组的值为：该节点的“全局地址idx“

e[M]，索引为：全局地址idx，值：节点序号

ne[M]，索引为：全局地址idx，值：全局地址idx

visited[N]，索引为：节点序号，值：true/false表示该节点是否被访问过

  1. 无向图，构建的时候，需要增加 a→ba\to b 的边，也要增加 b→ab\to a 的边，且M=2∗NM=2*N

  2. h[N] 存储的是每个邻接表的表头地址，初始化时，均为-1，Arrays.fill(h, -1)。可以用来判断链表的终止

    关于链表的模拟，查看笔记数组模拟单双链表

例题

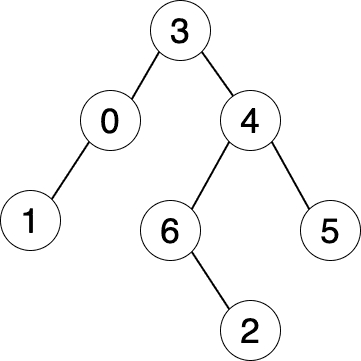
863. 二叉树中所有距离为 K 的结点

先将二叉树转为图，再进行 BFS\text{BFS}

1
2
3
4
5
6
7
8
9
10
11
12
13
public void build(TreeNode root) {
    if (root == null) return;
    if (root.left != null) {
        add(root.val, root.left.val);
        add(root.left.val, root.val);
        build(root.left);
    }
    if (root.right != null) {
        add(root.val, root.right.val);
        add(root.right.val, root.val);
        build(root.right);
    }
}

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
class Solution {
    static final int N = 510;
    static final int M = 2 * N;
    int idx = 0;
    int[] h = new int[N];
    int[] ne = new int[M];
    int[] e = new int[M];
    boolean[] visited = new boolean[N];
    void add(int a, int val) {
        e[idx] = val;
        ne[idx] = h[a];
        h[a] = idx++;
    }
    public List<Integer> distanceK(TreeNode root, TreeNode target, int k) {
        Arrays.fill(h, -1);
        idx = 0;
        build(root);
        int tt = target.val;
        visited[tt] = true;
        Queue<Integer> q = new LinkedList<>();
        q.offer(tt);
        List<Integer> res = new ArrayList<>();
        while (!q.isEmpty() && k >= 0) {
            int size = q.size();
            while (size-- > 0) {
                int cur = q.poll();
                if (k == 0) {
                    res.add(cur);
                    continue;
                }
                for (int i = h[cur]; i != -1; i = ne[i]) {
                    if (!visited[e[i]]) {
                        q.offer(e[i]);
                        visited[e[i]] = true;
                    }
                }
            }
            k--;
        }
        return res;
    }

    public void build(TreeNode root) {
        if (root.left != null) {
            add(root.val, root.left.val);
            add(root.left.val, root.val);
            build(root.left);
        }
        if (root.right != null) {
            add(root.val, root.right.val);
            add(root.right.val, root.val);
            build(root.right);
        }
    }
}

哈希表相关

见哈希表题目集锦

链表相关

头插法反转链表

1
2
3
4
5
6
7
8
9
10
11
ListNode* reverseList(ListNode* head) {
    ListNode* prev = nullptr;
    ListNode* curr = head;
    while (curr != nullptr) {
        ListNode* nextTemp = curr->next;
        curr->next = prev;
        prev = curr;
        curr = nextTemp;
    }
    return prev;
}

快慢指针

见快慢指针解决环形链表问题

快慢指针可以寻找链表的中间结点

新建一个前置节点dummy

例如，四个节点的情况

dummy–>4->[2]->1->3–>null

返回的midNode=[2]

五个节点的情况

dummy–>-1->5->[3]->4->0–>null

返回的midNode=[3]

1
2
3
4
5
6
7
8
9
ListNode findMid(ListNode head) {
       ListNode dummy = new ListNode(0, head);
       ListNode fast = dummy, slow = dummy;
       while (fast != null && fast.next != null) {
           fast = fast.next.next;
           slow = slow.next;
       }
       return slow;
   }

综合

  • 剑指 Offer II 026. 重排链表

    重排链表

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    class Solution {
        public void reorderList(ListNode head) {
            // 快慢指针找中点
            ListNode fast = head, slow = head, p = head;
            while (fast != null && fast.next != null) {
                fast = fast.next.next;
                slow = slow.next;
            }
            ListNode cur = slow.next;
            // 断环
            slow.next = null;
            // 翻转后半部分
            ListNode prev = null;
            while (cur != null) {
                ListNode next = cur.next;
                cur.next = prev;
                prev = cur;
                cur = next;
            }
            // 缝合两部分
            while (prev != null) {
                ListNode next1 = prev.next;
                ListNode next2 = p.next;
                prev.next = p.next;
                p.next = prev;
                prev = next1;
                p = next2;
            }

            return;
        }
    }

  • 剑指 Offer II 027. 回文链表

    • 注意空间复杂度，要满足 O(1)\Omicron(1)
    • 代码略

  • 25. K 个一组翻转链表

    还是翻转加指针定位，过程略微复杂

    代码

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    class Solution {
        public ListNode reverseKGroup(ListNode head, int k) {
            ListNode dummy = new ListNode(0, head);
            ListNode prev = dummy, tail = head;

            while (head != null) {
                // 指针定位，无论是快慢双指针，还是单指针定位，最好从prev节点开始
                tail = prev;
                int tt = k;
                while (tt-- > 0 && tail != null) tail = tail.next;
                // tail == null说明剩下的节点数不够K个，直接返回结果
                if (tail == null) return dummy.next;

                // 开始翻转
                ListNode nextNode = tail.next;
                ListNode[] temp = myReverse(head, tail);
                head = temp[0]; tail = temp[1];
                
                // 缝合
                tail.next = nextNode;
                prev.next = head;
                
                // 移动指针，开始翻转下一段K个节点
                prev = tail;
                head = nextNode;
            }
            return dummy.next;
        }
        public ListNode[] myReverse(ListNode head, ListNode tail) {
            ListNode prev = tail.next;
            ListNode cur = head;
            while (prev != tail) {
                ListNode nex = cur.next;
                cur.next = prev;
                prev = cur;
                cur = nex;
            }
            return new ListNode[]{tail, head};
        }
    }

  • 剑指 Offer II 077. 链表排序

    归并的思想

    完整代码

    由于是链表，不能随机访问，因此无法使用堆排和快排，只能使用归并排序

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    class Solution {
        public ListNode sortList(ListNode head) {
            return merge(head);
        }
        ListNode merge(ListNode list) {
            if (list == null) return null;
            if (list.next == null) return list;
            ListNode midNode = findMid(list);
            ListNode rightStart = midNode.next;
            midNode.next = null; // 不要忘记截断！！！！
            ListNode left = merge(list);
            ListNode right = merge(rightStart);
            return mergeListNode(left, right);
        }

        ListNode mergeListNode(ListNode x, ListNode y) {
            ListNode res =  new ListNode(0);
            ListNode p = res;
            while (x != null && y != null) {
                if (x.val < y.val) {
                    p.next = x;
                    x = x.next;
                } else {
                    p.next = y;
                    y = y.next;
                }
                p = p.next;
            }
            if (x != null) p.next = x;
            if (y != null) p.next = y;
            return res.next;
        }

        ListNode findMid(ListNode head) {
            ListNode dummy = new ListNode(0, head);
            ListNode fast = dummy, slow = dummy;
            while (fast != null && fast.next != null) {
                fast = fast.next.next;
                slow = slow.next;
            }
            return slow;
        }
    }

  • 23. 合并K个升序链表

    简单归并

    java完整代码

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    class Solution {
        public ListNode mergeKLists(ListNode[] lists) {
            return mergeList(lists, 0, lists.length - 1);
        }
        ListNode merge(ListNode[] lists, int l, int r) {
            if (l > r) return null;
            if (l == r) return lists[l];
            int mid = l + r >> 1;
            return mergerListNode(merge(lists, l, mid), merge(lists, mid + 1, r));
        }

        ListNode mergerListNode(ListNode l1, ListNode l2) {
            ListNode dummy = new ListNode(0);
            ListNode p = dummy;
            while (l1 != null && l2 != null) {
                if (l1.val < l2.val) {
                    p.next = l1;
                    l1 = l1.next;
                } else {
                    p.next = l2;
                    l2 = l2.next;
                }
                p = p.next;
            } 
            if (l1 != null) p.next = l1;
            else p.next = l2;
            return dummy.next;
        }

    }

数学计算

1. 整数除法

剑指 Offer II 001. 整数除法

题解参考：简单易懂Java/C++ /Python/js/go - 整数除法(剑指)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    // 时间复杂度：O(1)
    public int divide(int a, int b) {
        if (a == Integer.MIN_VALUE && b == -1)
            return Integer.MAX_VALUE;
        int sign = (a > 0) ^ (b > 0) ? -1 : 1;
        a = Math.abs(a);
        b = Math.abs(b); // 如果b= -2147483648 即-2^31. 
                         // abs(Integer.MIN_VALUE)的结果仍然为-2147483648
        int res = 0;
        for (int i = 31; i >= 0; i--) {
            // 1. 首先，右移的话，再怎么着也不会越界
            // 2. 其次，无符号右移的目的是：将 -2147483648 看成 2147483648

            // 注意，这里不能是 (a >>> i) >= b 而应该是 (a >>> i) - b >= 0
            // 这个也是为了避免 b = -2147483648，如果 b = -2147483648
            // 那么 (a >>> i) >= b 永远为 true，但是 (a >>> i) - b >= 0 为 false
            if ((a >>> i) - b >= 0) { // a >= (b << i)
                a -= (b << i);
                // 代码优化：这里控制 res 大于等于 INT_MAX
                // if (res > Integer.MAX_VALUE - (1 << i)) {
                //     return Integer.MIN_VALUE;
                // }
                res += (1 << i);
            }
        }
        // bug 修复：因为不能使用乘号，所以将乘号换成三目运算符
        return sign == 1 ? res : -res;
    }
}

学习位运算 和 边界控制的方法

总结：

  1. 对于 Math.abs()函数，取绝对值 Math.abs(Integer.MIN_VALUE)的结果为−2147483648-2147483648

  2. 第18行中原始代码是

    1
    a >= (b << i);

    但是存在几个问题：

    • bb左移可能会越界 -->改为aa右移：右移不会出现越界的情况。(a >> i) >= b;

    • 但是如果b为−2147483648-2147483648，即Integer.MIN_VALUE最小值，(a >> i) >= b永远为truetrue

    • 改为(a >> i) - b >= 0，

    • 如果aa为−2147483648-2147483648，取绝对值还是−2147483648-2147483648，右移是负数

    • 改为无符号右移 ，即(a >>> i) - b >= 0

0%