基于双向链表的一些数据结构设计问题

发表于 分类于 Artalk： loading...
设计 双向链表 哈希表 队列 LRU LFU

总结一下乐扣上的一些基于双向链表的设计题。

这类题目一般是中等难度起步，但是如果熟悉各种基础数据结构，思路灵活一点还是很容易解决的。

前言

我觉得双向链表是一个很灵活的数据结构。

  • 其一，双向链表删除任何节点的复杂度是 O(1)\Omicron(1) 的
  • 其二，双向链表可以在表头和表尾直接插入/删除节点，用来模拟队列和栈都很方便
  • 其三，双向链表也有链表的共同缺点——无法按照下标随机访问，但是在具体问题中，有时也可以结合哈希表实现以 O(1)\Omicron(1) 的复杂度访问特定节点

下面先来一个比较简单的开胃凉菜

LRU 缓存

设计思路

在之前的博文中也介绍过，LRU(Least Recently Used, 最近最久未使用)算法，在操作系统的页面调度中被使用，发生缺页中断时，如果驻留集已满，会选择将最长时间未被访问的页面进行置换

如何设计并实现LRU缓存呢？关键在于节点的淘汰机制，插入新节点时，当缓存容量达到上限(capacity)，需要将最长时间未被访问的节点移除，并放入新节点

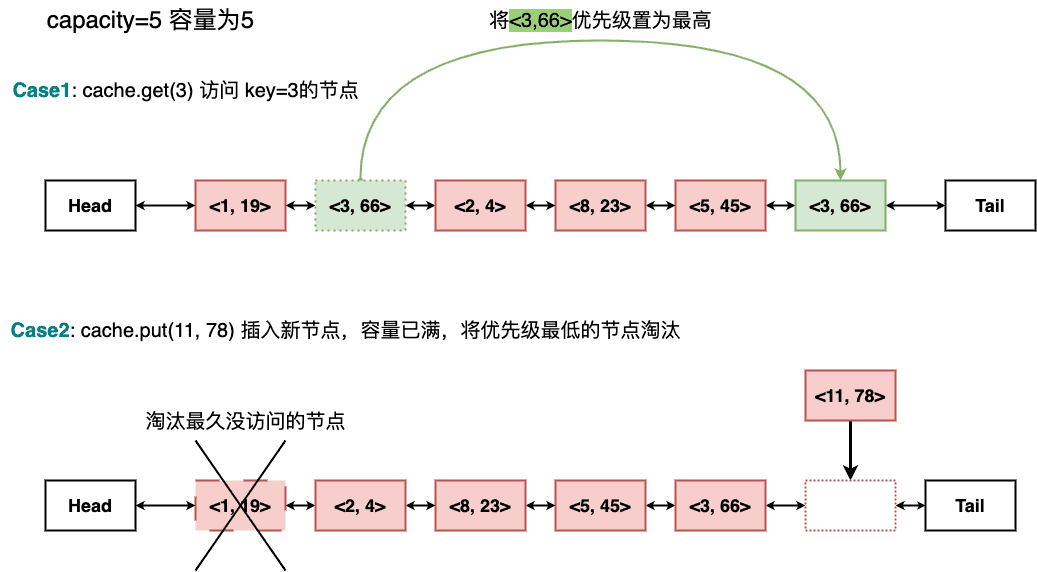
可以利用双向链表实现一个逻辑上的优先级队列，从表头到表尾优先级逐渐升高。

每当节点被访问（包括查询节点值和插入节点），都赋予该节点最高的优先级，即将该节点放到表尾部。

那么，表头也即队头的节点，既是优先级最低的节点，也是最长时间没有被访问的节点，也是被淘汰的节点（如果需要淘汰）

具体实现

具体实现上，本题存储的是键值对，通过哈希表保存键key和节点Node的映射，实现对节点的随机访问

每个节点除了要存储的<key>和<value>，还要保存两个指针，分别指向前一个节点和下一个节点

每当双向链表的节点被访问，更新优先级的操作在具体实现上，分为两步：1.删除原节点，2.将该节点插入表尾(队尾)

部分操作示意如下：

LRU

完整代码

题目描述

image-20230105151153422

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
class LRUCache {
    class Node {
        int key, val;
        Node prev, next;
        public Node(int key, int val) {
            this.key = key;
            this.val = val;
        }
        public Node() {
            this(-1, -1);
        }
    }
    class DoublyLinkedList {
        Node head, tail;
        public DoublyLinkedList() {
            this.head = new Node();
            this.tail = new Node();
            head.next = tail;
            tail.prev = head;
        }
        Node addLast(Node node) {
            node.prev = tail.prev;
            tail.prev.next = node;
            node.next = tail;
            tail.prev = node;
            return node;
        }
        void refresh(Node node) {
            delete(node);
            addLast(node);
        }
        Node delete(Node node) {
            node.prev.next = node.next;
            node.next.prev = node.prev;
            return node;
        }
        Node pollFirst() {
            Node t = head.next;
            delete(t);
            return t;
        }
    }
    Map<Integer, Node> store;
    DoublyLinkedList list;
    int capacity;
    public LRUCache(int capacity) {
        this.list = new DoublyLinkedList();
        this.store = new HashMap<>();
        this.capacity = capacity;
    }
    
    public int get(int key) {
        if (store.containsKey(key)) {
            Node node = store.get(key);
            list.refresh(node);
            return node.val;
        }
        return -1;
    }
    
    public void put(int key, int value) {
        if (store.containsKey(key)) {
            Node node = store.get(key);
            node.val = value;
            store.put(key, node);
            list.refresh(node);
        } else {
            if (store.size() == capacity) {
                Node t = list.pollFirst();
                store.remove(t.key);
            }
            Node node = new Node(key, value);
            store.put(key, node);
            list.addLast(node);
        }
        return ;
    }
}

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache obj = new LRUCache(capacity);
 * int param_1 = obj.get(key);
 * obj.put(key,value);
 */

关于时间复杂度，双向链表的节点删除/插入都是 O(1)\Omicron(1) 的，并且通过哈希表保存键和节点的映射，对于节点的访问也是 O(1)\Omicron(1)

因此，整体上 get() 和 put() 操作的时间复杂度均为 O(1)\Omicron(1)

接下来，是一道类似的题目

460. LFU 缓存

介绍

LFU(Least Frequently Used, 最近最不常用)算法，也是操作系统中页面调度算法的一种，与LRU不同的是，LFU算法淘汰的是最近访问频率最小的页面

举个夸张的例子，假设当前驻留集大小为3，已装入页面1，2，3。以下是访问序列。

1
1,3,1,3,1,3,1,3,2,[4]

访问到页面4时，发生缺页中断，此时驻留集已满，需要选择一个页面换出

如果按照LRU算法，最近最久未访问的页面是1，需要将页面1换出

但是按照LFU算法，页面2的访问次数是最少的，会将页面2换出

设计LFU缓存，要求实现LFUCache 类：

  • LFUCache(int capacity) - 用数据结构的容量 capacity 初始化对象
  • int get(int key) - 如果键 key 存在于缓存中，则获取键的值，否则返回 -1 。
  • void put(int key, int value) - 如果键 key 已存在，则变更其值；如果键不存在，请插入键值对。当缓存达到其容量 capacity 时，则应该在插入新项之前，移除最不经常使用的项。在此问题中，当存在平局（即两个或更多个键具有相同使用频率）时，应该去除 最近最久未使用 的键。

为了确定最不常使用的键，可以为缓存中的每个键维护一个 使用计数器 。使用计数最小的键是最不经常使用的键。

当一个键首次插入到缓存中时，它的使用计数器被设置为 1 (由于 put 操作)。对缓存中的键执行 get 或 put 操作，使用计数器的值将会递增。

函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

设计思路

关键在于淘汰策略，由于会先根据访问频率进行淘汰，因此可以将具有相同访问频率的节点集合到一起，同时记录最小访问频率。

当存在多个键的访问频率相同时，淘汰的是最久未使用的键，这部分和LRU算法思路是一致的，同样采用双向链表来存放。

那么，只需建立起访问频率和双向链表之间的映射，即一个访问频率对应一个双向链表。

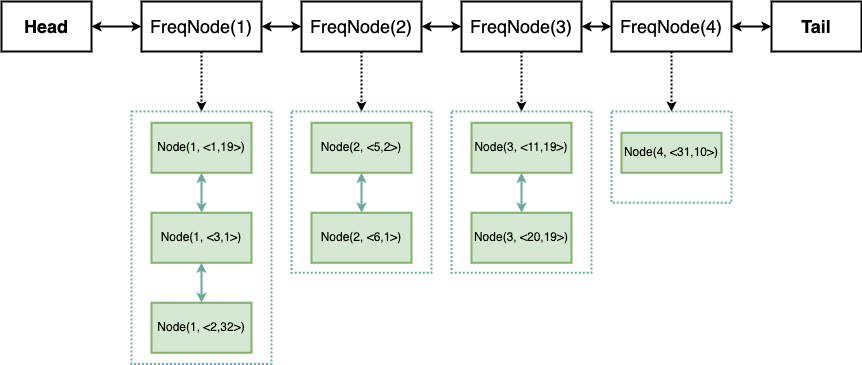
思路1：参照LRU的设计思路，频率之间也可以用双向链表组织起来，每个频率节点同时也代表一个双向链表，存放相同访问频率的数据节点

示意图如下（省略了子链表的头尾节点）

LFU-1

此法相当于双向链表套双向链表，还需要多创建一个哈希表来存储访问频率和FreqNode之间的映射，代码实现较繁琐。

这个设计思路中，最外层，访问频率用双向链表组织起来是没有必要的，因为我们只需要知道具有最小的访问频率的键即可

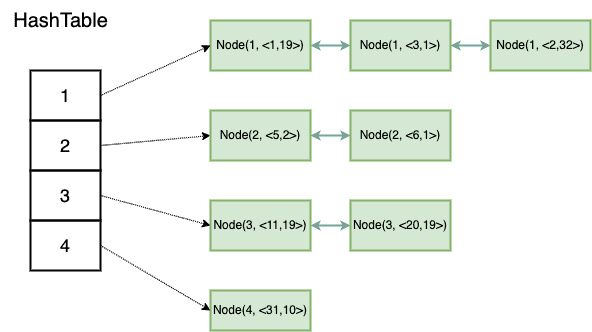
思路2：仅仅记录全局最小的访问频率，建立访问频率和双向链表之间的映射，直接用哈希表存储映射关系

这样做如何记录最小的访问频率（minFreq）呢？

  • 首先，新插入一个键值对，此节点的访问频率为1，那么此时全局最小的访问频率置为1
  • 如果当前双向链表对应的频率为minFreq，且经过操作，链表为空，那么minFreq直接加一即可。无论是查询键、更新键值对，都会引起访问频率的增加，则在前面所述情况下，minFreq + 1对应的双向链表一定存在

示意图如下

LFU-2

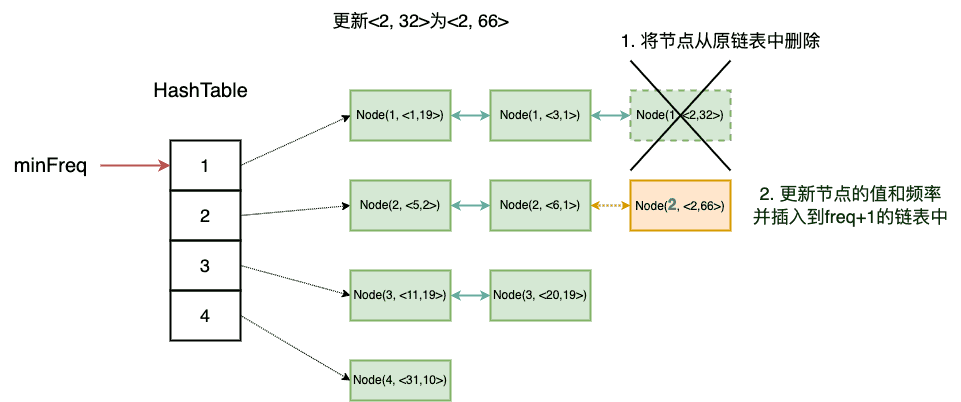
具体实现细节上，以更新键值对为例

LFU-2-1

无论是更新键值对还是查询键对应的值，都会引起节点的更新

更新代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public void refresh(Node node) {
    // 更新当前的node
    int curFreq = node.freq;
    var list = freqList.get(curFreq);
    list.delete(node); // 从当前频率表中删去node
    // 如果当前频率表空了，移除
    if (list.size == 0) { 
        if (curFreq == minFreq) minFreq++; // 如果当前频率是最小频率，更新最小频率
        freqList.remove(curFreq);
    }
    curFreq++; // 频率更新
    node.freq = curFreq;
    // 更新频率表
    var target = freqList.getOrDefault(curFreq, new DoubleLinkedList());
    target.addLast(node);
    freqList.put(curFreq, target);
    // 更新键值对存储
    store.put(node.key, node);
}

完整代码

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
class LFUCache {
    class Node {
        int val, freq, key;
        Node prev, next;
        public Node() {
            this(0, -1, -1);
        }
        public Node(int freq, int key, int val) {
            this.freq = freq; 
            this.key = key;
            this.val = val;
        }
    }  
    class DoubleLinkedList {
        Node head, tail;
        int size;
        public DoubleLinkedList() {
            this.head = new Node();
            this.tail = new Node();
            head.next = tail;
            tail.prev = head;
            this.size = 0;
        }
        Node addLast(Node node) {
            node.prev = tail.prev;
            tail.prev.next = node;
            node.next = tail;
            tail.prev = node;
            size++;
            return node;
        }
        Node peekFirst() {
            return head.next;
        }
        Node peekLast() {
            return tail.prev;
        }
        Node delete(Node node) {
            node.prev.next = node.next;
            node.next.prev = node.prev;
            size--;
            return node;
        }
    }  

    Map<Integer, Node> store;
    Map<Integer, DoubleLinkedList> freqList;
    int capacity, minFreq;
    public LFUCache(int capacity) {
        this.store = new HashMap<>();
        this.freqList = new HashMap<>();
        this.capacity = capacity;
        this.minFreq = 0;
    }
    
    public void refresh(Node node) {
        // 更新当前的node
        int curFreq = node.freq;
        var list = freqList.get(curFreq);
        list.delete(node); // 从当前频率表中删去node
        if (list.size == 0) { 
            // 如果当前频率表空了，移除
            if (curFreq == minFreq) minFreq++; // 如果当前频率是最小频率，更新最小频率
            freqList.remove(curFreq);
        }
        curFreq++; // 频率更新
        node.freq = curFreq;
        // 更新频率表
        var target = freqList.getOrDefault(curFreq, new DoubleLinkedList());
        target.addLast(node);
        freqList.put(curFreq, target);
        // 更新键值对存储
        store.put(node.key, node);
    }

    public int get(int key) {
        if (capacity == 0) return -1;
        if (!store.containsKey(key)) return -1;
        Node node = store.get(key);
        refresh(node);
        return node.val;
    }
    
    public void put(int key, int value) {
        if (capacity == 0) return ;
        if (store.containsKey(key)) { // key已经存在
            Node node = store.get(key);
            node.val = value; // 更新键值对
            refresh(node);
        } else {
            // 插入新的键值对
            // 达到容量上限时，删除 最不常使用 的键值对
            if (store.size() == capacity) { 
                var list = freqList.get(minFreq);
                Node t = list.delete(list.peekFirst());
                if (list.size == 0) {
                    freqList.remove(minFreq);
                }
                store.remove(t.key); // 删除store中的键值对
            }
            // 插入新值
            Node node = new Node(1, key, value);
            var list = freqList.getOrDefault(1, new DoubleLinkedList());
            list.addLast(node);
            store.put(key, node);
            freqList.put(1, list);
            minFreq = 1;
        }
    }
}

其他相关例题

432. 全 O(1) 的数据结构

题目描述

image-20230105201536390

简要分析

本题要设计的数据结构和LFU缓存很像，主要区别在于getMaxKey()和getMinKey()两个函数，只要求返回任意一个计数最大或最小的字符串，并无特殊要求。这样，对于同一个计数下的字符串的存放结构要求就不是很高，为了插入和删除的效率，可以用一个哈希集合来存放这些字符串

另一个不同点在于，本题需要记录最大的计数和最小的计数，采用类似LFU思路2的方法是无法保证在 O(1)\Omicron(1) 的复杂度下维护这两个变量的。

因此这里直接将不同的计数用双向链表组织起来，同时再用一个哈希表保存字符串和链表节点之间的映射

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
class AllOne {
    class Node {
        int cnt;
        Set<String> set;
        Node prev, next;
        public Node() {
            this(0);
        }
        public Node(int cnt) {
            this.cnt = cnt;
            this.set = new HashSet<>();
        }
    }
    Node head, tail;
    Map<String, Node> store;
    public AllOne() {
        this.head = new Node(-1000);
        this.tail = new Node(-1000);
        head.next = tail;
        tail.prev = head;
        this.store = new HashMap<>();
    }
    void clear(Node node) {
        if (node.set.size() == 0) {
            node.prev.next = node.next;
            node.next.prev = node.prev;
        }
    }
    public void inc(String key) {
        if (store.containsKey(key)) {
            Node node = store.get(key);
            int cnt = node.cnt;
            if (node.next.cnt != cnt + 1) {
                Node t = new Node(cnt + 1);
                t.next = node.next;
                node.next.prev = t;
                t.prev = node;
                node.next = t;
            }
            node.next.set.add(key);
            store.put(key, node.next);
            node.set.remove(key);
            clear(node);
        } else {
            if (head.next.cnt != 1) {
                Node t = new Node(1);
                t.next = head.next;
                head.next.prev = t;
                t.prev = head;
                head.next = t;
            }
            head.next.set.add(key);
            store.put(key, head.next);
        }
        
    }
    
    public void dec(String key) {
        // 系统保证key一定存在
        Node node = store.get(key);
        int cnt = node.cnt;
        if (cnt == 1) {
            node.set.remove(key);
            clear(node);
            store.remove(key);
            return ;
        }
        if (node.prev.cnt != cnt - 1) {
            Node t = new Node(cnt - 1);
            t.prev = node.prev;
            node.prev.next = t;
            t.next = node;
            node.prev = t;
        }
        node.prev.set.add(key);
        store.put(key, node.prev);
        node.set.remove(key);
        clear(node);
    }
    
    public String getMaxKey() {
        var s = tail.prev.set;
        for (var x : s) return x;
        return "";
    }
    
    public String getMinKey() {
        var s = head.next.set;
        for (var x : s) return x;
        return "";
    }
}

1429. 第一个唯一数字

题目描述

给定一系列整数，插入一个队列中，找出队列中第一个唯一整数。

实现 FirstUnique 类：

  • FirstUnique(int[] nums) 用数组里的数字初始化队列。
  • int showFirstUnique() 返回队列中的 第一个唯一 整数的值。如果没有唯一整数，返回 -1。
  • void add(int value) 将 value 插入队列中。

简要分析

本题思路相对简单一点，使用一个记录频次的哈希表来判断插入的整数是否是唯一的

然后将符合条件的整数，插入到双向链表的表尾

PS：双向链表在这里是模拟一个先入先出的队列，那为什么不直接用队列呢？

由于不断插入新的值，可能会导致队列中的元素不符合「唯一」值个条件，需要频繁的删除，而双向链表删除任意节点的复杂度是 O(1)\Omicron(1) 的

具体实现起来就简单了

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
class FirstUnique {
    class Node {
        int val;
        Node prev, next;
        public Node(int val) {this.val = val;}
    }
    Node head, tail;
    Map<Integer, Node> store;
    Map<Integer, Integer> cnt;
    void addLast(Node node) {
        node.prev = tail.prev;
        tail.prev.next = node;
        node.next = tail;
        tail.prev = node;
        return ;
    }
    void delete(Node node) {
        node.prev.next = node.next;
        node.next.prev = node.prev;
    }
    Node peekFirst() {
        return head.next;
    }
    public FirstUnique(int[] nums) {
        this.cnt = new HashMap<>();
        this.head = new Node(-1);
        this.tail = new Node(-1);
        head.next = tail;
        tail.prev = head;
        this.store = new HashMap<>();
        
        for (int x : nums) {
            insert(x);
        }
    }
    
    void insert(int val) {
        if (cnt.containsKey(val)) {
            if (store.containsKey(val)) {
                delete(store.get(val));
                store.remove(val);
            }
            cnt.put(val, cnt.get(val) + 1);
        } else {
            cnt.put(val, 1);
            Node t = new Node(val);
            addLast(t);
            store.put(val, t);
        }
    }
    public int showFirstUnique() {
        if (head.next != tail) {
            return peekFirst().val;
        }
        return -1;
    }
    
    public void add(int x) {
        insert(x);
    }
}

1472. 设计浏览器历史记录

题目描述

image-20230105204206312

简要分析

本题思路较为赤裸，需要在浏览记录中前进和后退，并且可能会需要连续删除元素，双向链表无疑是最适合的数据结构

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
class BrowserHistory {
    // 双向链表
    class Node {
        Node prev, next;
        String val;
        public Node(String str) { val = str; }
    }
    class DoublyLinkedList {
        Node head, tail;
        public DoublyLinkedList() {
            this.head = new Node("@");
            this.tail = new Node("@");
            head.next = tail;
            tail.prev = head;
        }
        Node addLast(String url) {
            Node t = new Node(url);
            t.prev = tail.prev;
            tail.prev.next = t;
            t.next = tail;
            tail.prev = t;
            return t;
        }
        Node peekLast() {
            return tail.prev;
        }
        Node insertNode(Node cur, String val) {
            Node t = new Node(val);
            cur.next = t;
            t.prev = cur;
            t.next = tail;
            tail.prev = t;
            return t;
        }
    }
    DoublyLinkedList store;
    Node cur;
    public BrowserHistory(String homepage) {
        this.store = new DoublyLinkedList();
        this.cur = this.store.addLast(homepage);
    }
    
    public void visit(String url) {
        cur = store.insertNode(cur, url);
        return ;
    }
    
    public String back(int steps) {
        while (cur.prev != store.head && steps-- > 0) cur = cur.prev; 
        return cur.val;
    }
    
    public String forward(int steps) {
        while (cur.next != store.tail && steps-- > 0) cur = cur.next;
        return cur.val;
    }
}

716. 最大栈

本题和双向链表关系不大，个人觉得不错，贴出来

题目介绍及代码

image-20230105205144336

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class MaxStack {
    class Node {
        int v;
        Node prev, next;
        public Node(int v) { this.v = v; }
    }
    
    TreeMap<Integer, List<Node>> mp;
    Deque<Node> store;
    public MaxStack() {
        this.mp = new TreeMap<>();
        this.store = new LinkedList<>();
    }
    
    public void push(int x) {
        store.offerLast(new Node(x));
        Node t = store.peekLast();
        if (!mp.containsKey(x)) {
            mp.put(x, new ArrayList<Node>());
        }
        mp.get(x).add(t);
        return ;
    }
    
    public int pop() {
        int t = store.pollLast().v;
        var list = mp.get(t);
        list.remove(list.size() - 1);
        if (list.isEmpty()) mp.remove(t);
        return t;
    }
    
    public int top() {
        return store.peekLast().v;
    }
    
    public int peekMax() {
        return mp.lastKey();
    }
    
    public int popMax() {
        int t = peekMax();
        var list = mp.get(t);
        var node = list.remove(list.size() - 1);
        store.remove(node);
        if (list.isEmpty()) mp.remove(t);
        return t;
    }
}