线段树学习笔记

线段树，常用来维护区间信息，属于二叉搜索树

本文主要是学习笔记（来自@木子喵neko），侧重代码实现。

简述

线段树是平衡二叉树，采用递归的形式，将当前区间划分成左右两个区间，直至区间大小为1。每个区间保存一个或者多个需要的数值，例如，区间的和、区间的最大值。采用树的形式存放这些区间，就构成了一颗二叉树——线段树。

线段树的维护，用小区间的值来更新大区间，时间复杂度是 $\Omicron(\log N)$ 的

可以使用线段树解决的问题需要满足「区间加法」：对于 $[left,right]$ 区间的解，可以由 $[left,k]$ 和 $[k, right]$ 的解合并求出，其中 $k$ 为分割点

例如：区间求和问题，区间最值问题等

使用细节

步骤

1. 建树
2. 单点修改/区间修改
3. 区间查询

其中区间修改会用到「懒标记」

存储方式

数组存储，类似堆的方式。例如：序号从1开始，记当前节点为 $u$ ，其左孩子为 $2*u$ ，其右孩子为 $2*u+1$ ，其父节点为 $u/2$

PS: 数组大小一般开到 $4*n$ ，防止越界

单点修改

假设要修改下标为 $i$ 的数据，从根节点向下深搜

如果当前节点的左儿子的区间包含了 $i$ ，就访问左儿子；否则访问右儿子

直到搜索到的区间 $[L,R]$ 满足 $L=R$ ，即搜索到了只包含这个数据的节点，修改这个节点

然后向上更新包含此数据的大区间的值

区间查询（仅有单点修改）

1. 如果待查询区间「覆盖」当前区间，直接返回当前区间的值
2. 如果查询区间和左儿子有交集，递归搜索左儿子
3. 如果查询区间和右儿子有交集，递归搜索右儿子
4. 最后合并处理两边查询的数据

区间修改

如果按照常规思路，向下递归修改所有节点，复杂度很高

这里引入「懒标记」：

将此区间标记，表示这个区间的值已经更新，但是它的子区间还没更新，更新的信息就是标记里存放的值

---

步骤：

1. 先判断修改区间的覆盖情况

   1. 如果要修改的区间「完全覆盖」当前区间，直接更新这个区间，打上lazy标记

   2. 如果没有完全覆盖，且当前区间有lazy标记，则先下传lazy标记到子区间，再清除当前区间的lazy标记

2. 如果修改区间和左儿子有交集，递归搜索左儿子

3. 如果修改区间和右儿子有交集，递归搜索右儿子

4. 最后更新当前区间的值

Ps：多次修改时，才会使用到下传操作

区间查询（涉及区间修改，有懒标记）

1. 如果要查询的区间完全覆盖当前区间，直接返回当前区间的值
2. 如果没有完全覆盖，有标记的话，下传lazy标记（更新左右儿子，并打上lazy标记）
3. 如果查询区间和左儿子有交集，递归搜索左儿子
4. 如果查询区间和右儿子有交集，递归搜索右儿子
5. 最后合并左右两侧的查询数据

代码实现

代码实现来自宫水三叶

这里以「区间求和」为例

节点创建

一般用内部类（结构体）的形式存储节点，节点编号从1开始

static final int N = (int)1e4+10;
class Node {
    int l, r, v, add; // 'add' 为懒标记的值
    public Node(int l, int r) {
        this.l = l;
        this.r = r;
    }
}
Node[] tr = new Node[N * 4]; // 防止越界

建树

void build(int u, int l, int r) ，三个传入参数分别是当前节点的编号，左孩子节点的编号，右孩子节点的编号

void build(int u, int l, int r) {
    tr[u] = new Node(l, r);
    if (l != r) { // 当前节点代表一个区间
        int mid = l + r >> 1; // 二分当前区间
        build(u << 1, l, mid); // 递归构建左孩子节点
        build(u << 1 | 1, mid + 1, r); // 递归构建右孩子节点
    }
}

代码中有个小细节，u << 1 | 1 就是 2 * u + 1，是其右孩子编号。因为 u 左移一位后，最低位肯定是0，对最低位赋1，就相当于整体加1。

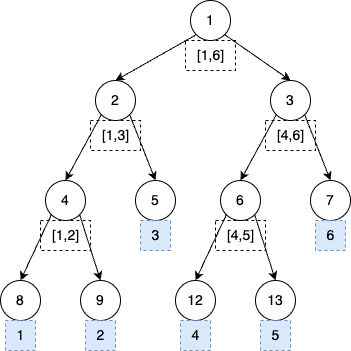
画图模拟一下 build(1, 1, 6) 构建 $[1,6]$ 区间的过程

区间修改

解释见代码注释

void update(int u, int l, int r, int v) {
    // 如果要修改的区间[l,r] 完全覆盖当前节点的区间
    // 则直接更新值，并更新lazy标记
    if (l <= tr[u].l && tr[u].r <= r) { 
        tr[u].v += v;
        tr[u].add += v;
    } else {
        pushdown(u); // 先「下传」懒标记
        int mid = tr[u].l + tr[u].r >> 1;
        // 如果和左儿子的区间有交集，递归搜索左儿子
        if (l <= mid) update(u << 1, l, r, v); 
        // 右儿子同理
        // 写成 if (r >= mid + 1) 也行
        if (r > mid) update(u << 1 | 1, l, r, v);
        // 「上传」结果，更新当前区间的值
        pushup(u);
    }
}

其中，「下传」过程其实就是将当前节点的懒标记信息，加到两个儿子节点的懒标记上，并且在此时，根据懒标记的值，更新子节点的值，最后清除当前节点的懒标记

代码如下

void pushdown(int u) {
    int add = tr[u].add;
    tr[u << 1].add += add;
    tr[u << 1].v += add;
    tr[u << 1 | 1].add += add;
    tr[u << 1 | 1].v += add;
    tr[u].add = 0; // 最后不要忘记清除当前节点的懒标记
}

上传操作，就是用左右子节点的值更新当前节点的值

void pushup(int u) {
    tr[u].v = tr[u << 1].v + tr[u << 1 | 1].v;
}

区间查询

区间查询和区间修改的代码实现很相似

int query(int u, int l, int r) {
    if (l <= tr[u].l && tr[u].r <= r) return tr[u].v;
    
    pushdown(u); // 下传lazy标记
    int ans = 0;
    int mid = tr[u].l + tr[u].r >> 1;
    if (l <= mid) ans += query(u << 1, l, r);
    if (r > mid) ans += query(u << 1 | 1, l, r);
    return ans;
}

例题

1109. 航班预订统计

本题目属于「区间修改，单点查询」问题，差分是最优解

class Solution {
    /**
    线段树代码
    **/
    public int[] corpFlightBookings(int[][] bs, int n) {
        build(1, 1, n); // 建树
        for (int[] bo : bs) {
            update(1, bo[0], bo[1], bo[2]); // 区间[bo[0], bo[1]]上加bo[2]
        }
        int[] ans = new int[n];
        for (int i = 0; i < n; i++) {
            ans[i] = query(1, i + 1, i + 1); // 注意编号是从1开始的
        }
        return ans;
    }
}

动态开点

简析

动态开点的含义是，事先不进行树的构建，在进行update()和query()时，再进行节点的创建。问题在于，由于更新和查询并不一定是连续的，无法通过序号（2*u 和 2*u+1）的方式访问左右孩子。

这里的解决方法是：

@【区间和专题の前缀和】线段树（动态开点）运用题

将节点 $tr[u]$ 的左右节点所在 tr 数组的下标进行存储，分别记为 ls 和 rs 属性。对于 $tr[u].ls == 0$ 和 $tr[u].rs == 0$ 则是代表子节点尚未被创建，当需要访问到它们，而又尚未创建的时候，则将其进行创建。

相比于常规方式，动态开点的线段树实现上：

1. Node 节点不再保存当前节点代表的区间 $[l,r]$ ，转而保存当前节点的左右孩子节点的编号（也即在tr数组中的下标，同样从1开始）
2. 由于更新和查询操作都是用递归实现的，当前节点代表的区间信息 $[lc,rc]$ ，可以直接放到传入参数列表中

代码实现

以「区间求和」为例

节点定义

动态开点下，空间复杂度是 $\Omicron(m\log n)$ 的，这里猜测常数为 $\text{4}$ ，确定上界

class Node {
    int ls, rs, add, v;
}
int N = (int)1e9, M = 4 * 400 * 30, idx = 1;
Node[] tr = new Node[M];

idx 代表节点在数组中的编号，从 $\text{1}$ 开始

节点创建

当前节点的ls/rs == 0，视作孩子节点尚未创建的标志，则进行创建

void lazyCreate(int u) {
    if (tr[u] == null) tr[u] = new Node();
    if (tr[u].ls == 0) {
        tr[u].ls = ++cnt;
        tr[tr[u].ls] = new Node();
    }
    if (tr[u].rs == 0) {
        tr[u].rs = ++cnt;
        tr[tr[u].rs] = new Node();
    }
}

区间修改

void update(int u, int lc, int rc, int l, int r, int v) {
    if (l <= lc && rc <= r) {
        tr[u].v += v;
        tr[u].add += v;
        return;
    }
    lazyCreate(u);
    pushdown(u);
    int mid = lc + rc >> 1;
    if (l <= mid) update(tr[u].ls, lc, mid, l, r, v);
    if (r > mid) update(tr[u].rs, mid + 1, rc, l, r, v);
    pushup(u);
    return ;
}

区间查询

int query(int u, int lc, int rc, int l, int r) {
    if (l <= lc && r >= rc) return tr[u].v;
    lazyCreate(u);
    pushdown(u);
    int ans = 0;
    int mid = lc + rc >> 1;
    if (l <= mid) ans += query(tr[u].ls, lc, mid, l, r);
    if (r > mid) ans += query(tr[u].rs, mid + 1, rc, l, r);
    return ans;
}

「下传/上传」操作

void pushdown(int u) {
    int add = tr[u].add;
    tr[tr[u].ls].v += add; tr[tr[u].ls].add += add;
    tr[tr[u].rs].v += add; tr[tr[u].rs].add += add;
    tr[u].add = 0;
}
void pushup(int u) {
    tr[u].v = tr[tr[u].ls].v + tr[tr[u].rs].v;
}

例题

732. 我的日程安排表 III

当 k 个日程安排有一些时间上的交叉时（例如 k 个日程安排都在同一时间内），就会产生 k 次预订。

给你一些日程安排 [start, end) ，请你在每个日程安排添加后，返回一个整数 k ，表示所有先前日程安排会产生的最大 k 次预订。

提示：

• 0 <= start < end <= 109
• 每个测试用例，调用 book 函数最多不超过 400次

记 $n=10^9\ , m = 400$ ，如果采取常规方式事先创建空数组，空间复杂度为 $\Omicron(n)$ ，空间占用会溢出，采取动态开点的方式

完整代码

「区间最值」问题

class MyCalendarThree {
    class Node {
        int ls, rs, add, max;
    }
    int N = (int)1e9, M = 4 * 400 * 30, cnt = 1;
    Node[] tr = new Node[M];
    void update(int u, int lc, int rc, int l, int r, int v) {
        if (l <= lc && rc <= r) {
            tr[u].add += v;
            tr[u].max += v;
            return ;
        }
        lazyCreate(u);
        pushdown(u);
        int mid = lc + rc >> 1;
        if (l <= mid) update(tr[u].ls, lc, mid, l, r, v);
        if (r > mid) update(tr[u].rs, mid + 1, rc, l, r, v);
        pushup(u);
    }
    int query(int u, int lc, int rc, int l, int r) {
        if (l <= lc && rc <= r) return tr[u].max;
        lazyCreate(u);
        pushdown(u);
        int mid = lc + rc >> 1, ans = 0;
        if (l <= mid) ans = query(tr[u].ls, lc, mid, l, r);
        if (r > mid) ans = Math.max(ans, query(tr[u].rs, mid + 1, rc, l, r));
        return ans;
    }
    void lazyCreate(int u) {
        if (tr[u] == null) tr[u] = new Node();
        if (tr[u].ls == 0) {
            tr[u].ls = ++cnt;
            tr[tr[u].ls] = new Node();
        }
        if (tr[u].rs == 0) {
            tr[u].rs = ++cnt;
            tr[tr[u].rs] = new Node();
        }
    }
    void pushdown(int u) {
        tr[tr[u].ls].add += tr[u].add; tr[tr[u].rs].add += tr[u].add;
        tr[tr[u].ls].max += tr[u].add; tr[tr[u].rs].max += tr[u].add;
        tr[u].add = 0;
    }
    void pushup(int u) {
        tr[u].max = Math.max(tr[tr[u].ls].max, tr[tr[u].rs].max);
    }
    public int book(int start, int end) {
        update(1, 1, N + 1, start + 1, end, 1);
        return query(1, 1, N + 1, 1, N + 1);
    }
}

关于上限设定 int M = 4 * 400 * 30，由于动态开点的方式，每一次操作最多创建 $\log n$ 级别的节点，因此空间复杂度为 $\Omicron(m\log n)$ 。计算上界时，这里猜测常数为4（即

$k=\lim_{n\to\infty}\frac{Space}{m\log n}$），因此设定为 4 * 400 * 30

相关例题

@宫水三叶

线段树代码很长，且常数很大，实际表现不算很好。只有不得不写「线段树」的时候，我们才考虑线段树。

如何抉择？

• 数组不变，区间查询：前缀和、树状数组、线段树；
• 数组单点修改，区间查询：树状数组、线段树；
• 数组区间修改，单点查询：差分、线段树；
• 数组区间修改，区间查询：线段树。

因此，最好是遇到「区间修改+区间查询」时才用线段树来解决

宫水三叶的参考题单

待更新…

面试题 16.17. 连续数列

借鉴了pushup的思想合并区间

给定一个整数数组，找出总和最大的连续数列，并返回总和。

输入： [-2,1,-3,4,-1,2,1,-5,4]
输出： 6
解释： 连续子数组 [4,-1,2,1] 的和最大，为 6。

分治的思想，逐渐切分区间，然后从底向上合并每个区间

对于每个区间维护四个变量

• ls，以区间左端点为左边界的最大连续数列的和
• rs，以区间右端点为右边界的最大连续数列的和
• sum，当前区间的和
• maxSum， 当前区间内的最大连续数列的和，即所求

如何维护见示意图

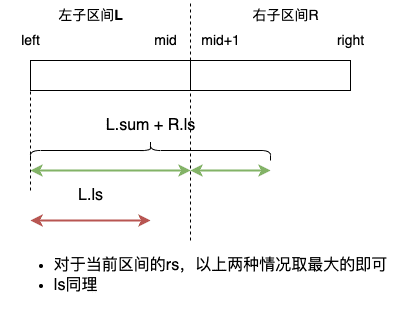
维护 rs 和 ls

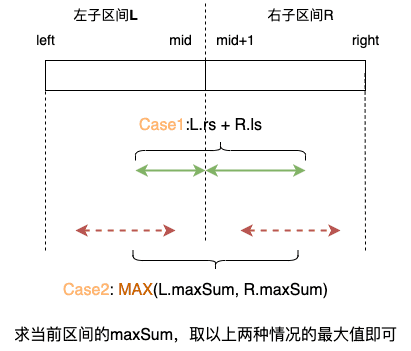
维护 maxSum

代码实现

class Solution {
    class Node {
        int ls, rs, sum, maxSum;
        public Node(int ls, int rs, int sum, int maxSum) {
            this.ls = ls; this.rs = rs; this.sum = sum; this.maxSum = maxSum;
        }
        public Node() { this(0, 0, 0, 0); }
    }
    public int maxSubArray(int[] nums) {
        // 分治
        return helper(nums, 0, nums.length - 1).maxSum;
    }
    Node helper(int[] q, int l, int r) {
        if (l == r) return new Node(q[l], q[r], q[l], q[l]);
        int mid = l + r >> 1;
        Node left = helper(q, l, mid);
        Node right = helper(q, mid + 1, r);
        return pushup(left, right);
    }
    Node pushup(Node l, Node r) {
        Node node = new Node();
        node.sum = l.sum + r.sum;
        node.ls = Math.max(l.ls, l.sum + r.ls);
        node.rs = Math.max(r.rs, r.sum + l.rs);
        node.maxSum = Math.max(Math.max(l.maxSum, r.maxSum), l.rs + r.ls);
        return node;
    }
}

参考资料

• 线段树｜OI Wiki
• 线段树｜Wiki
• 宫水三叶的刷题日记