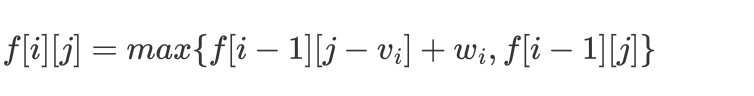相比01背包,完全背包问题:不限制物品的使用数量
yxc闫式dp分析法-视频链接
acwing 3. 完全背包问题
题目
![image-20220528175458609]()
求解思路
化零为整
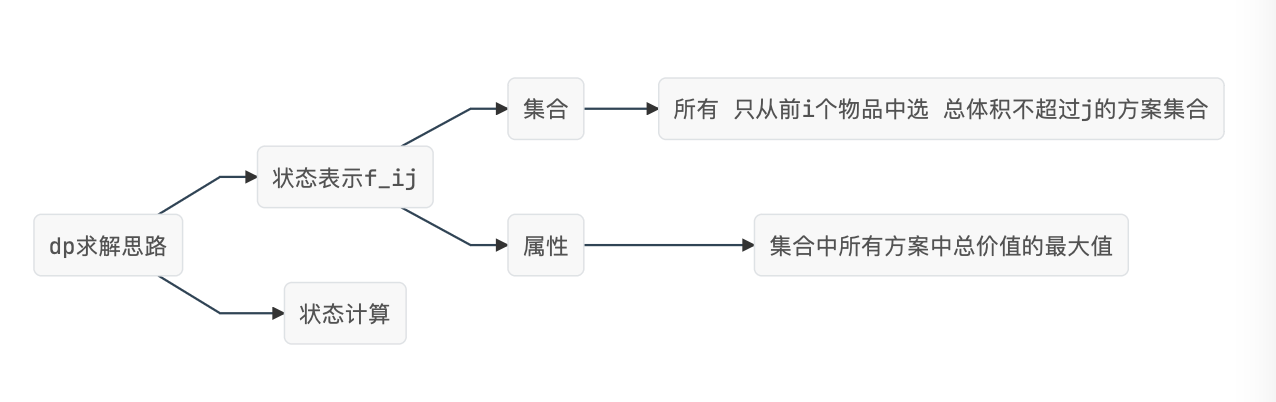
关于状态表示
![image-20220313182143815]()
至于状态计算,对于 f[i][j] ,第 i 个物品,选0个,选1个,选2个…选k个
即
f[i][j]=max{f[i−1][j],f[i−1][j−vi]+wi,f[i−1][j−2vi]+2wi…f[i−1][j−kvi]+kwi}
而
f[i][j−vi]=max{f[i−1][j−vi],f[i−1][j−2vi]+wi…f[i−1][j−kvi]+(k−1)wi}
对比以上两个式子
可以推导出
f[i][j]=max{f[i−1][j],f[i][j−vi]+wi}
即完全背包问题的状态转移方程
对比01背包问题,仅仅一个 i−1 的差别
01背包问题的状态转移方程
![image-20220313191240744]()
解题
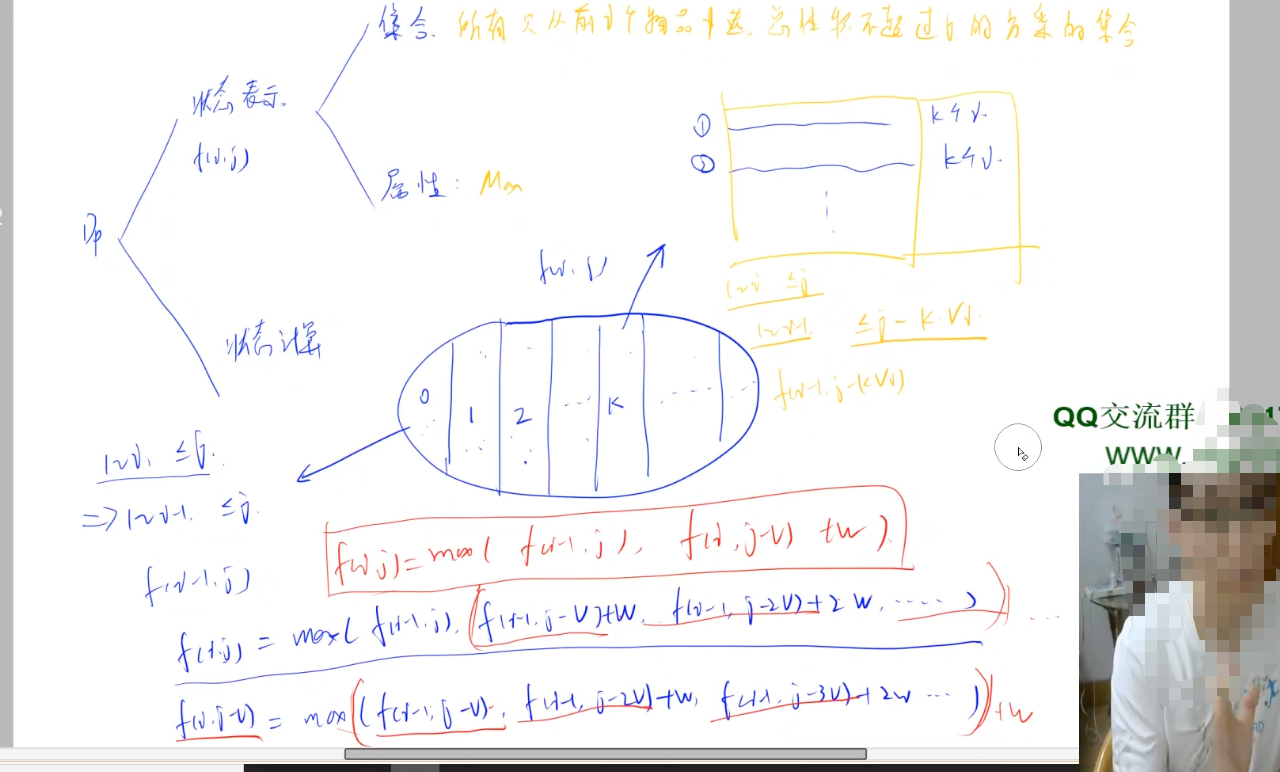
y总板书
![image-20220313185550241]()
结合01背包问题的注意事项-1来理解。
![image-20220313185638194]()
也可手动模拟一下。
因此,在完全背包问题中,只需要在之前基础上将遍历顺序改成从 vi 到 m 即可
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| import java.util.Scanner;
public class Test01Package2 {
private static int N = 1010;
private static int w[] = new int[N];
private static int v[] = new int[N];
private static int f[] = new int[N];
public static void main(String[] args) {
Scanner cin = new Scanner(System.in);
int n = cin.nextInt();
int m = cin.nextInt();
for (int i = 1; i <= n; i++) {
v[i] = cin.nextInt();
w[i] = cin.nextInt();
}
for (int i = 1; i <= n; ++i) {
for (int j = v[i]; j <=m; ++j) {
f[j] = Math.max(f[j], f[j-v[i]] + w[i]);
}
}
System.out.println(f[m]);
}
}
|
@2022年 4月12日 星期二 15时17分10秒 CST
背包类刷题经验-通关剑
如果要算两个三位数字相乘,直接算很难。
dp的思路其实就是以列竖式的形式计算,从集合的角度来看
135×76810945 10260
计数DP-整数划分
题目描述
![image-20220528180640166]()
个人认为,可以归为完全背包问题的特殊情况
背包的容量为 n ,有 n 种物品,每种物品不限制使用数量,求恰好装满背包的方案数量
解题思路
按照完全背包的方式来思考
状态表示 f[i][j]
正整数集合
1, 2, 3…n
- 集合: 从前 i 个正整数中选,加和为 j 的方案集合
- 属性: 集合中方案的数量
状态计算:f[i][j]=f[i−1][j]+f[i][j−i]
解释: 这里,第 i 个正整数,值为 i
f[i][j−i] 表示选取了第 i 个整数,然后再从前 i 个整数中选,加和为 j-i 的方案数量,因为每一个整数不限制选取数量,属于完全背包问题,i 可以重复选取
代码
以下代码进一步优化了空间占用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| import java.util.*;
class Main{
static final int M = (int)1e9+7;
static final int N = (int)1e3+10;
static final int[] dp = new int[N];
public static void main(String[] args) {
Scanner cin = new Scanner(System.in);
int n = cin.nextInt();
dp[0] = 1;
for (int i = 1; i <= n; ++i) {
for (int j = i; j <= n; ++j) {
dp[j] = (dp[j] + dp[j - i]) % M;
}
}
System.out.println(dp[n]);
}
}
|
另一种思路
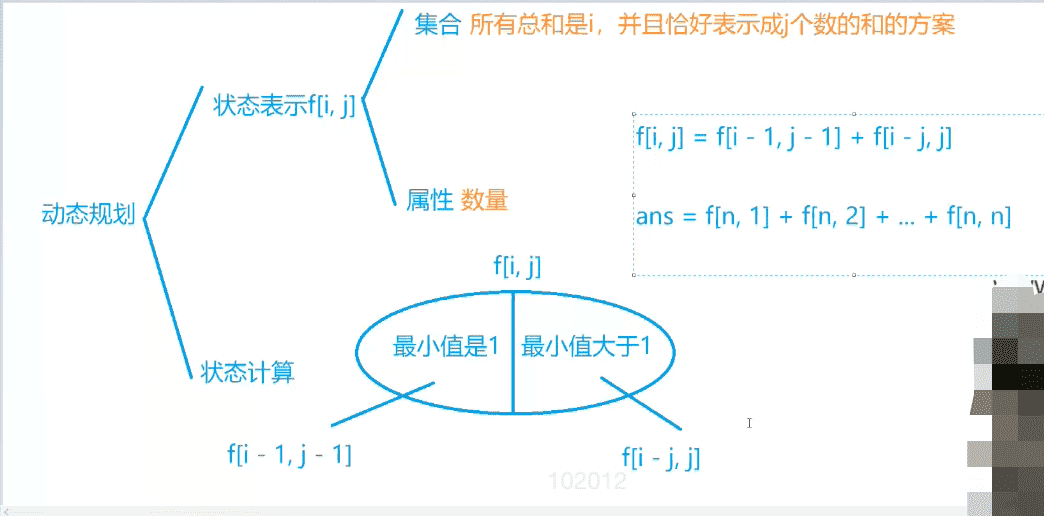
Y总板书
![image-20220528212618560]()
解释
转移方程
f[i][j]=f[i−1][j−1]+f[i−j][j]
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| import java.util.*;
class Main{
static final int M = (int)1e9+7;
static final int N = (int)1e3+10;
static final int[][] dp = new int[N][N];
public static void main(String[] args) {
Scanner cin = new Scanner(System.in);
int n = cin.nextInt();
dp[0][0] = 1;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= i; ++j) {
dp[i][j] = (dp[i - 1][j - 1] + dp[i - j][j]) % M;
}
}
for (int i = 1; i <= n; ++i) dp[n][i] = (dp[n][i] + dp[n][i - 1]) % M;
System.out.println(dp[n][n]);
}
}
|
其他可以用完全背包解决的问题
问题描述
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
示例
1
2
3
4
5
6
7
| 输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
|
简要分析
dp[i][j]
转移方程
dp[i][j]=max{dp[i-1][j], dp[i][j-i]∗i}
同样的,滚动数组优化空间占用后 dp[j]=max{dp[j], dp[j-i]∗i}
代码实现
注意初值设置,和题目条件:k>=2 至少两个正整数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution {
static final int INF = 0x3f3f3f3f;
public int integerBreak(int n) {
int[] dp = new int[n + 1];
Arrays.fill(dp, -INF);
dp[0] = 1;
for (int i = 1; i < n; ++i) {
for (int j = i; j <= n; ++j) {
dp[j] = Math.max(dp[j], dp[j - i] * i);
}
}
return dp[n];
}
}
|
问题描述
给你两个整数 num 和 k ,考虑具有以下属性的正整数多重集:
每个整数个位数字都是 k 。
所有整数之和是 num 。
返回该多重集的最小大小,如果不存在这样的多重集,返回 -1 。
注意:
- 多重集与集合类似,但多重集可以包含多个同一整数,空多重集的和为
0 。 - 个位数字 是数字最右边的数位。
简要分析
dp[i][j]
- 表示的集合:只考虑前 i 个合法整数,加和为 j 的方案集合
- 属性:集合中「包含最少元素的方案」的元素个数
转移方程
dp[i][j]=max{dp[i-1][j], dp[i][j-i]+1}
滚动数组优化空间占用后 dp[j]=max{dp[j], dp[j-i]+1}
代码实现
关于初值设置
dp[0] = 0, 其余赋最大值INF ,可以保证dp[num]一定是从dp[0]处转移过来的
如此,dp[num] 代表的就是加和「恰好等于num」的方案中的最小元素数(如果dp[num]!=INF)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| class Solution {
static final int INF = 0x3f3f3f3f;
public int minimumNumbers(int num, int k) {
List<Integer> nums = new ArrayList<>();
for (int i = 1; i <= num; ++i) {
if (i % 10 == k) nums.add(i);
}
int n = nums.size();
int[] dp = new int[num + 1];
Arrays.fill(dp, INF);
dp[0] = 0;
for (int i = 0; i < n; ++i) {
int cur = nums.get(i);
for (int j = cur; j <= num; ++j) {
dp[j] = Math.min(dp[j], dp[j - cur] + 1);
}
}
return dp[num] > INF / 2 ? -1 : dp[num];
}
}
|
其他例题
接下来贴两道简单题,但体现了完全背包思路的两种最常见用法
给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。
请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。
假设每一种面额的硬币有无限个。
题目数据保证结果符合 32 位带符号整数
示例
1
2
3
4
5
6
7
| 输入:amount = 5, coins = [1, 2, 5]
输出:4
解释:有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
|
求的是方案个数,初始化 dp[0]=1, 因为凑成0元,什么也不选也是一种有效方案
1
2
3
4
5
6
7
8
9
10
11
12
| class Solution {
public int change(int amount, int[] coins) {
int[] dp = new int[amount + 1];
dp[0] = 1;
for (int x : coins) {
for (int i = x; i <= amount; ++i) {
dp[i] += dp[i - x];
}
}
return dp[amount];
}
}
|
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例
1
2
3
| 输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
|
求的是填满背包所需的物品个数,初始化 dp[0]=0 ,凑成0元不需要任何硬币
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution {
static final int INF = 0x3f3f3f3f;
public int coinChange(int[] coins, int amount) {
int[] dp = new int[amount + 1];
Arrays.fill(dp, INF);
dp[0] = 0;
for (int x : coins) {
for (int i = x; i <= amount; ++i) {
dp[i] = Math.min(dp[i], dp[i - x] + 1);
}
}
return dp[amount] > INF / 2 ? -1 : dp[amount];
}
}
|
唯一需要注意的是,所求的是恰好凑成目标金额的最小硬币个数,因此需要保证最终结果 dp[amount] 一定是从 dp[0] 转移过来的
初始化 dp[0] = 0 ,其他设置为 INF ,这样做可以保证,如果 dp[amount] != INF,那结果一定合法
即 dp[amount] 就是容量恰好等于amount时的最小物品数量,而不是容量小于等于amount时的物品数量
📔博文图谱
提及本博文的链接