「转载」BitMap的JAVA实现
前言
原文链接:BitMap的JAVA实现
相关概念
基础类型
在java中:
1 | byte -> 8 bits -->1字节 |
位运算符
在java中,int数据底层以补码形式存储。int型变量使用32bit存储数据,其中最高位是符号位,0表示正数,1表示负数,可通过Integer.toBinaryString()转换为bit字符串,
1 | // 若最高的几位为0则不输出这几位,从为1的那一位开始输出 |
左移<<
5<<2=20
1 | 首先会将5转为2进制表示形式: 0000 0000 0000 0000 0000 0000 0000 0101 |
右移>>
5>>2=1
1 | 还是先将5转为2进制表示形式:0000 0000 0000 0000 0000 0000 0000 0101 |
无符号右移>>>
5>>>3
我们知道在Java中int类型占32位,可以表示一个正数,也可以表示一个负数。正数换算成二进制后的最高位为0,负数的二进制最高为为1。对于2进制补码的加法运算,和平常的计算一样,而且符号位也参与运算,不过最后只保留32位。
1 | -5换算成二进制: 1111 1111 1111 1111 1111 1111 1111 1011 |
位与&
第一个操作数的的第n位于第二个操作数的第n位如果都是1,那么结果的第n为也为1,否则为0
1 | 5转换为二进制:0000 0000 0000 0000 0000 0000 0000 0101 |
位或|
第一个操作数的的第n位于第二个操作数的第n位只要有一个为1则为1,否则为0
1 | 5转换为二进制:0000 0000 0000 0000 0000 0000 0000 0101 |
对于移位运算,例如将x左移/右移n位,如果x是byte、short、char、int,n会先模32(即n=n%32),然后再进行移位操作。可以这样解释:int类型为32位,移动32位(或以上)没有意义。
同理若x是long,n=n%64。
左移和右移代替乘除
1 | a=a*4; |
可以改为
1 | a=a<<2; |
说明:
除2 = 右移1位 乘2 = 左移1位
除4 = 右移2位 乘4 = 左移2位
除8 = 右移3位 乘8 = 左移3位
…
类比十进制中的满十进一,向左移动小数点后,数字就会缩小十倍,在二进制中满二进一,进行右移一次相当于缩小了2两倍,右移两位相当于缩小了4倍,右移三位相当于缩小了8倍。通常如果需要乘以或除以2的n次方,都可以用移位的方法代替。
**实际上,只要是乘以或除以一个整数,均可以用移位的方法得到结果,**如:
a=a*9
分析a*9可以拆分成a*(8+1)即a*8+a*1, 因此可以改为: a=(a<<3)+a
a=a*7
分析a*7可以拆分成a*(8-1)即a*8-a*1, 因此可以改为: a=(a<<3)-a
关于除法读者可以类推, 此略。
【注意】由于+/-运算符优先级比移位运算符高,所以在写公式时候一定要记得添加括号,不可以 a = a*12 等价于 a = a<<3 + a<<2; 要写成a = (a<<3)+(a <<2 )。
与运算代替取余
1 | 31转换为二进制:011111,0,31 |
31转换为二进制后,低位值全部为1,高位全为0。所以和其进行与运算,高位和0与,结果是0,相当于将高位全部截取,截取后的结果肯定小于等于31,低位全部为1,与1与值为其本身,所以相当于对数进行了取余操作。
进制转换
0x开头表示16进制,例如:0x2表示:2,0x2f表示480开头表示8进制,例如:02表示:2,010表示8
1 | Integer.toHexString(int i) // 十进制转成十六进制 |
BitMap实现原理
在java中,一个int类型占32个字节,我们用一个int数组来表示时未new int[32],总计占用内存32*32bit,现假如我们用int字节码的每一位表示一个数字的话,那么32个数字只需要一个int类型所占内存空间大小就够了,这样在大数据量的情况下会节省很多内存。
具体思路:
1个int占4字节即4*8=32位,那么我们只需要申请一个int数组长度为 int tmp[1+N/32]即可存储完这些数据,其中N代表要进行查找的总数,tmp中的每个元素在内存在占32位可以对应表示十进制数0~31,所以可得到BitMap表:
tmp[0]:可表示0~31
tmp[1]:可表示32~63
tmp[2]可表示64~95
…
那么接下来就看看十进制数如何转换为对应的bit位:
假设这40亿int数据为:6,3,8,32,36,…,那么具体的BitMap表示为:
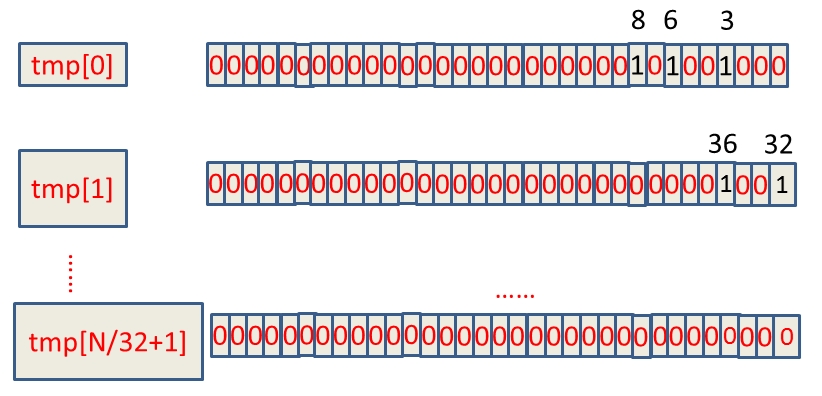
如何判断int数字在tmp数组的哪个下标,这个其实可以通过直接除以32取整数部分,例如:整数8除以32取整等于0,那么8就在tmp[0]上。另外,我们如何知道了8在tmp[0]中的32个位中的哪个位,这种情况直接mod上32就ok,又如整数8,在tmp[0]中的第8 mod上32等于8,那么整数8就在tmp[0]中的第八个bit位(从右边数起)。
BitMap源码
1 | private long length; |
BitMap应用
- BitMap小小变种:2-BitMap。
看个小场景:在3亿个整数中找出不重复的整数,限制内存不足以容纳3亿个整数。
对于这种场景我可以采用2-BitMap来解决,即为每个整数分配2bit,用不同的0、1组合来标识特殊意思,如00表示此整数没有出现过,01表示出现一次,11表示出现过多次,就可以找出重复的整数了,其需要的内存空间是正常BitMap的2倍,为:3亿*2/8/1024/1024=71.5MB。
具体的过程如下:
扫描着3亿个整数,组BitMap,先查看BitMap中的对应位置,如果00则变成01,是01则变成11,是11则保持不变,当将3亿个整数扫描完之后也就是说整个BitMap已经组装完毕。最后查看BitMap将对应位为11的整数输出即可。
- 已知某个文件内包含一些电话号码,每个号码为8位数字,统计不同号码的个数。
8位最多99 999 999,大概需要99m个bit,大概10几m字节的内存即可。 (可以理解为从0-99 999 999的数字,每个数字对应一个Bit位,所以只需要99M个Bit=12MBytes,这样,就用了小小的12M左右的内存表示了所有的8位数的电话)
BitMap问题
BitMap 的思想在面试的时候还是可以用来解决不少问题的,然后在很多系统中也都会用到,算是一种不错的解决问题的思路。
但是 BitMap 也有一些局限,因此会有其它一些基于 BitMap 的算法出现来解决这些问题。
- 数据碰撞。比如将字符串映射到 BitMap 的时候会有碰撞的问题,那就可以考虑用 Bloom Filter 来解决,Bloom Filter 使用多个 Hash 函数来减少冲突的概率。
- 数据稀疏。又比如要存入(10,8887983,93452134)这三个数据,我们需要建立一个 99999999 长度的 BitMap ,但是实际上只存了3个数据,这时候就有很大的空间浪费,碰到这种问题的话,可以通过引入 Roaring BitMap 来解决。
参考链接