「随笔」原地哈希&&位运算相关例题

关于原地哈希和位运算相关题目，简单记录

有些时候，待处理数组元素具有一定特点，例如值在一个区间([1,N])内，可以利用数组本身作为哈希表，降低空间占用

引子

41. 缺失的第一个正数

给出一个未排序的整数数组，找到其中没有出现的最小正整数

例如：nums = [3,4,-1,1]，结果为 2

要求：

• 时间复杂度 $\Omicron(n)$

• 空间复杂度 $\Omicron(1)$，常数级别额外空间

分析

如果没有空间占用的要求，很容易想到，维护一个哈希集合，从 1 开始遍历，找到集合中第一个没有出现的正整数

class Solution {
    public int firstMissingPositive(int[] nums) {
        Set<Integer> set = new HashSet<>();
        for (int x : nums) set.add(x);
        int l = 1, r = Integer.MAX_VALUE;
        int num = 1;
        while (num <= Integer.MAX_VALUE) {
            if (!set.contains(num)) return num;
            num ++;
        }
        return num;
    }
}

但是这个方案空间占用不符合要求，考虑原地哈希

将数组 $nums$ 本身当作一个哈希表，数组的值 $nums[i]$ 看作哈希表的下标

这个哈希表需要维护的功能是，储存「值为 $i$ 的整数是否存在」这个信息，可以通过打标记来实现，如何打标记之后再说

那么，对于数组中 $i$ 位置 $nums[i]$ 来说，它有两个功能

1. 本来的功能：储存这个值
2. 表示 $hash[nums[j]]$，即 $nums[j]$ 这个整数存在

并且这两个功能不能冲突！！

解决方案（如何打标记？）：

对于 $nums[i]$ ，如何表示其存在性？

将 $nums[nums[i]]$ 设为其绝对值的负数，这样对于 $nums$ 的每一个元素

• $nums[i]$ 的绝对值代表这个位置真正保存的数值

• 如果 $nums[i]$ 小于零，则说明 $nums$ 数组存在值为 $i$ 的元素，否则不存在

代码实现

具体实现上，有一些细节需要注意

1. 下标是从 0 开始的，而元素的目标值域是从 1 开始的，要减 1
2. 数组中存在小于零的数，可以将这些位置标记成值域之外的值，使无效化。由于 nums 作为哈希表使用时，数值跨度最大为 n = nums.length ，从 1 开始，则最大值为 n，标记为 n+1 即可

class Solution {
    public int firstMissingPositive(int[] nums) {
        int n = nums.length;
        for (int i = 0; i < n; ++i) {
            // nums作为哈希表时，值域为[1,n]
            // 小于0的数，标记为 n+1，无效化
            if (nums[i] <= 0) nums[i] = (n + 1);
        }
        for (int i = 0; i < n; ++i) {
            // 每一位的绝对值才是真正保存的值
            int x = Math.abs(nums[i]);
            if (x <= n) { // 在哈希表的值域内
                // 将数值的下标的位置的值，标记为负数，代表该值存在
                // 实际编码时，要减1，因为下标是从0开始的
                nums[x - 1] = -Math.abs(nums[x - 1]);
            }    
        }
        for (int i = 0; i < n; ++i) {
            // 一旦i位置的值大于零，说明i+1这个值不存在
            if (nums[i] > 0) return i + 1;
        }
        return n + 1;
    }
}

面试题 17.19. 消失的两个数字

给定一个数组，包含从 1 到 N 的所有整数，但是缺少了两个数字，找到消失的两个数字

要求空间复杂度为 $\Omicron(1)$

例子

输入: [1]
输出: [2,3]

分析

同样的，将 $nums$ 数组本身当作哈希表使用

对于 $nums[i]$ ，如何通过打标记，记录其存在性？

方案：将 $nums[\bold{nums[i]}]$ 设为其绝对值的负数。

这样对于 $nums$ 的每一个元素

• $nums[i]$ 的绝对值代表这个位置真正保存的数值

• 如果 $nums[i]$ 小于零，则说明 $nums$ 数组存在值为 $i$ 的元素，否则不存在

代码

*此代码仅作示意，实际空间占用为 $\Omicron(n)$

class Solution {
    public int[] missingTwo(int[] nums) {
        int n = nums.length;
        int[] q = new int[n + 2];
        System.arraycopy(nums, 0, q, 0, n);
        q[n] = n+10;
        q[n + 1] = n+10;
        for (int i = 0; i < n + 2; ++i) {
            int cur = Math.abs(q[i]);
            if (cur <= n + 2) {
                q[cur - 1] = -Math.abs(q[cur - 1]);
            }
        }
        int[] res = new int[2];
        for (int idx = 0, i = 0; i < n + 2; ++i) {
            if (idx >= 2) break;
            if (q[i] > 0) res[idx++] = i + 1;
        }

        return res;
    }
}

空间占用O(1)的代码实现

由于所需哈希表值域为 [1,n+2] ，要保持常数级别的额外空间占用，则开辟两个元素的空间，来实现对原数组的拓展

top[2]

class Solution {
    public int[] missingTwo(int[] q) {
        int n = q.length;
        int[] top = new int[]{n+10, n+10};
        int[] res = new int[2];
        for (int i = 0; i < n; ++i) {
            int cur = Math.abs(q[i]);
            if (cur <= n + 2) {
                if (cur >= n + 1) {
                    top[cur - n - 1] = -Math.abs(top[cur - n - 1]);
                } else {
                    q[cur - 1] = -Math.abs(q[cur - 1]);
                }
            }
        }
        for (int idx = 0, i = 0; i < n + 2; ++i) {
            if (idx >= 2) break;
            if (i < n ? q[i] > 0 : top[i - n] > 0) res[idx++] = i + 1;
        }
        return res;
    }
}

位运算解决方案

本题也可以用位运算解决，主要用到了关于异或的两个重要性质

• (1).x ^ x = 0
• (2).x ^ 0 = x

异或计算满足交换律

设 $nums$ 数组长度为 $n$，则 $N = n + 2$，如何找到 $[1,N]$ 中缺失的 $x_1$ 和 $x_2$ ？

解决方案：

将这 $2n+2$ 个元素连续求异或，得到 $x$

$x=nums[0]\oplus nums[1]\oplus nums[2]\dots \oplus nums[n-1]\oplus1\oplus 2 \dots\oplus N$

这 $2n+2$ 个数可以分为两类：1. 缺失的 $x_1,x_2$ 2.其他未缺失的

第 2. 类数在异或计算中均会出现两次，根据性质(1).其结果为0

由于 $x_1 \neq x_2$ ，因此结果 $x$ 中至少有一个数位的值为 $1$

lowbit = x & (-x) 表示 $x$ 的最低有效位，即最低为1的数位，记为第 $l$ 位，数值上为lowbit=1 << l

由于此数位为1只能是 $x_1$ 和 $x_2$ 贡献的（一个该数位为 $0$，另一个为 $1$，异或结果才能是 $1$ ），可以根据 lowbit 对数字分类：

根据第 $l$ 个数位为 $0$ 还是为 $1$ ，分成两类

• 对于任意一个在 $nums$ 中出现过一次的数字，其在 $2n+2$ 个数中出现两次，两个数会被包含在同一个类中
• 对于两个缺失的数字 $x_1$ 和 $x_2$ ，只出现一次，会被分到不同类中

因此，将 $2n+2$ 个数的每一类分别进行异或计算，由于 $x \oplus x = 0$ ，得到的异或结果

恰好是 $x_1$ 和 $x_2$

代码实现

class Solution {
    public int[] missingTwo(int[] nums) {
        int n = nums.length;
        int x = 0;
        for (int num : nums) x ^= num;
        for (int num = 1; num <= n + 2; ++num) x ^= num;
        // x = x1 ^ x2
        int lowbit = x & (-x);
        int x1 = 0, x2 = 0;
        for (int num : nums) {
            if ((num & lowbit) == 0) x1 ^= num;
            else x2 ^= num;
        }
        for (int num = 1; num <= n + 2; ++num) {
            if ((num & lowbit) == 0) x1 ^= num;
            else x2 ^= num;
        }
        return new int[]{x1,x2};
    }
}

与面试题17.19相似->645. 错误的集合

原地哈希

如出一辙，只不过本题目中哈希表的值域正好为 $[1,n]$ ，无需开辟额外空间

class Solution {
    public int[] findErrorNums(int[] nums) {
        int n = nums.length;
        int dup = -1, lost = -1;
        for (int i = 0; i < n; ++i) {
            int index = Math.abs(nums[i]) - 1;
            if (nums[index] < 0) dup = index + 1; // 已经有标记了，说明为重复元素
            else {
                // 打标记
                nums[index] = -Math.abs(nums[index]);
            }
        }
        for (int i = 1; i <= n; ++i) {
            if (nums[i - 1] > 0) {
                lost = i; // 无标记，说明为丢失元素
                break;
            }
        }
        return new int[]{dup, lost};
    }
}

位运算

和上一题的位运算解决方案思路基本一致

nums=[1,2,2,4]
[1,2,3,4] 
x = 1^2^2^4^1^2^3^4

同样的，按照 $2n$ 个数字异或结果 $x$ 的最低有效位，进行分类

丢失的数字记为 $dup$ ，重复的数字记为 $lost$ ，其余数字均出现了偶数次，不影响异或结果

$dup$ 和 $lost$ 出现奇数次，会被分到不同类中

class Solution {
    public int[] findErrorNums(int[] nums) {
        int n = nums.length;
        int x = 0;
        int x1 = 0, x2 = 0;
        // 求 xor
        for (int i = 1; i <= n; ++i) x ^= i;
        for (int num : nums) x ^= num;
        int lowBit = x & (-x);
        // 根据lowBit分类
        for (int i = 1; i <= n; ++i) {
            if ((i & lowBit) == 0) x1 ^= i;
            else x2 ^= i;
        }
        for (int num : nums) {
            if ((num & lowBit) == 0) x1 ^= num;
            else x2 ^= num;
        }
        // 如果nums存在x1，说明x1是重复的那个，否则是x2
        for (int num : nums) {
            if (num == x1) return new int[]{x1, x2};
        }
        return new int[]{x2, x1};
    }
}

其他题目，位运算相关

287. 寻找重复数

给定一个包含 $n + 1$ 个整数的数组 $nums$ ，其数字都在 $[1, n]$ 范围内（包括 $1$ 和 $n$ ），可知至少存在一个重复的整数。

假设 $nums$ 只有 一个重复的整数 ，返回 这个重复的数 。

你设计的解决方案必须 不修改 数组 $nums$ 且只用常量级 $\Omicron(1)$ 的额外空间。

注意：

• nums 中 只有一个整数 出现 两次或多次 ，其余整数均只出现 一次
• 也就是说存在 [2,2,2,2] 这种样例

分析

不能修改原数组，就不能用原地哈希来做

原地哈希

class Solution {
    public int findDuplicate(int[] nums) {
        int n = nums.length;
        for (int i = 0; i < n; ++i) {
            int cur = Math.abs(nums[i]);
            if (nums[cur - 1] < 0) return cur;
            else {
                nums[cur - 1] = -Math.abs(nums[cur - 1]);
            }
        }
        return -1;
    }
}

常量级别额外空间，也不能使用HashMap容器来做

HashMap做法

class Solution {
    public int findDuplicate(int[] nums) {
        Map<Integer, Integer> mp = new HashMap<>();
        for (int x : nums) {
            int cnt = mp.getOrDefault(x, 0);
            cnt++;
            mp.put(x, cnt);
        }
        for (Map.Entry<Integer, Integer> entry : mp.entrySet()) {
            if (entry.getValue() > 1) return entry.getKey();
        }
        return -1;
    }
}

尝试从位运算的角度去寻找解决思路

为了分析方便，之后举例均是，一个数字出现两次，其余数字出现一次。例如:

nums = [1,3,4,2,2]

n = 4, [1,2,3,4]

nums 数组包含 [1,n] 的所有整数，其中有一个数字出现了至少两次

拆成一个个数位去分析，如何才能还原出这个出现至少两次的数字呢？

记当前数位为 $i$ ，$nums$ 中出现两次的数字为 $x$

$[1,n]$ 所有数字，第 $i$ 位上的 $1$ 的出现次数记为 $x_1$ ；$nums$ 数组所有数字第 $i$ 位上的 $1$ 的个数记为 $x_2$

如果 $x$ 的第 $i$ 位为 $1$ 的话，则一定有 $x_2 = x_1 + 1$

更一般的题设条件下，有 $x_2 > x_1$

详细的分析可以参见乐扣的官方题解，思路类似

举例模拟

nums数组	1	3	4	2	2	x2	x1	x
第1位	0	0	1	0	0	1	1	0
第2位	0	1	0	1	1	3	2	1
第3位	1	1	0	0	0	2	2	0
(从左向右)								x=2

以上例子的 $x=2$ ，第2个数位为 $1$ ，有 $x_2>x_1$

代码实现

先求出最高数位，再依次求出每一位的 $x_1$ 和 $x_2$ ，比较后得出 $x$ 相应数位的值

class Solution {
    public int findDuplicate(int[] nums) {
        // 位运算
        int n = nums.length, ans = 0;
        int bitMax = 17; // n的范围 (1, 10^5)
        // 求出最高位，这里是从右向左看的
        while (((n - 1) >> bitMax & 1) == 0) {
            bitMax -= 1;
        }
        for (int bit = 0; bit <= bitMax; ++bit) {
            int x1 = 0, x2 = 0;
            for (int i = 0; i < n; ++i) {
                if (i >= 1 && ((i >> bit & 1) == 1)) x1++;
                if ((nums[i] >> bit & 1) == 1) x2++;
            }
            if (x2 > x1) {
                ans |= (1 << bit);
            }
        }
        return ans;
    }
}

本题最优解法

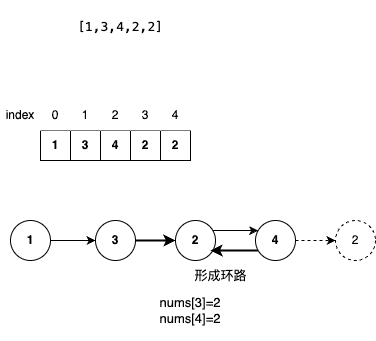
利用 $nums$ 数组构建一个图，图的每条边都是由 $i\to nums[i]$ 构成。

如果存在重复数字，那么会有多个位置指向这个重复的数字 $x$ ，则一定会形成环路

那么这个环路的入口，就是要求的答案

则可以使用快慢指针来求出环路入口，具体原理参见之前的博客:快慢指针解决环形链表问题

代码实现

class Solution {
    public int findDuplicate(int[] nums) {
        // 不修改数组--原地哈希 x
        // 常量级别额外空间--哈希表 x
        int slow = 0, fast = 0;
        while (true) {
            slow = nums[slow];
            fast = nums[nums[fast]];
            if (slow == fast) break;
        }
        fast = 0;
        while (slow != fast) {
            slow = nums[slow];
            fast = nums[fast];
        }
        return fast;
    }
}

二分查找

二分查找思路

class Solution {
    public int findDuplicate(int[] nums) {
        // 二分查找
        int n = nums.length;
        int l = 1, r = n - 1;
        while (l < r) {
            int mid = l + r >> 1;
            int cnt = 0;
            // 统计比当前数字mid小的数字个数
            for (int i = 0; i < n; ++i) {
                if (nums[i] <= mid) cnt++;
            }
            if (cnt > mid) r = mid;
            else l = mid + 1;
        }
        return l;
    }
}

类似例题

剑指 Offer II 070. 排序数组中只出现一次的数字

Solution

mid ^ 1 是将mid的二进制表示最低位反转

• 如果mid是偶数，mid ^ 1就是mid+1
• 如果mid是奇数，mid ^ 1就是mid-1

class Solution {
    public int singleNonDuplicate(int[] nums) {
        int n = nums.length;
        int l = 0, r = n - 1;
        while (l < r) {
            int mid = l + r >> 1;
            if (nums[mid] == nums[mid ^ 1]) l = mid + 1;
            else r = mid;
        }
        return nums[r];
    }
}

---

位运算相关问题，首先要熟悉相关基础知识，其次要学习数位DP的思想，从数位的角度去分析问题，利用在数位上的特点去突破