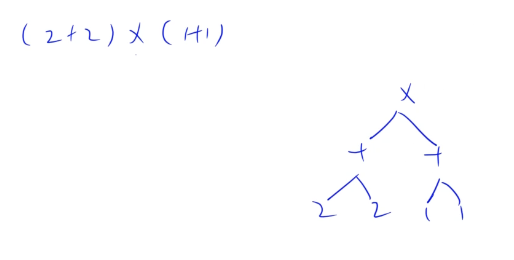表达式求值-栈

发表于 2021-11-15 更新于 2023-01-11 Artalk： loading...

栈中缀表达式后缀表达式

栈的基本应用，表达式求值相关问题

表达式求值

acwing 3302. 表达式求值

题目描述

给定一个表达式，其中运算符仅包含 +,-,*,/（加减乘整除），可能包含括号，请你求出表达式的最终值。

算法基于中缀表达式，利用两个辅助栈：符号栈和数字栈。

例如： $(2+2)\times(1+1)$

表达式树，叶节点为数字，非叶节点为运算符。

后缀表达式(也即对表达式树进行后序遍历)： 2 2 + 1 1 + x，

结合后缀表达式便于理解。

算法流程

扫描中缀表达式字符串str，对于每个ch：

如果ch代表数字，存入数字栈num
如果ch是左括号(，直接存入符号栈op
如果ch是右括号)，将op中的符号依次出栈，与num栈顶数字进行计算，直到op栈顶为左括号(，并将左括号弹出栈
如果ch是加减乘除符号+ - * / ，
- 若op栈顶计算符的优先级大于或者等于当前ch代表的计算符，循环：计算符出栈，计算值
- 直到op为空或者op栈顶为左括号(
- 完成循环后，将当前ch存入op栈顶

完成扫描后，如果op栈不为空，则将操作符依次出栈，计算值。

关于算法流程的第4步，进入循环的条件，op栈顶的运算符优先级要是大于或者等于ch

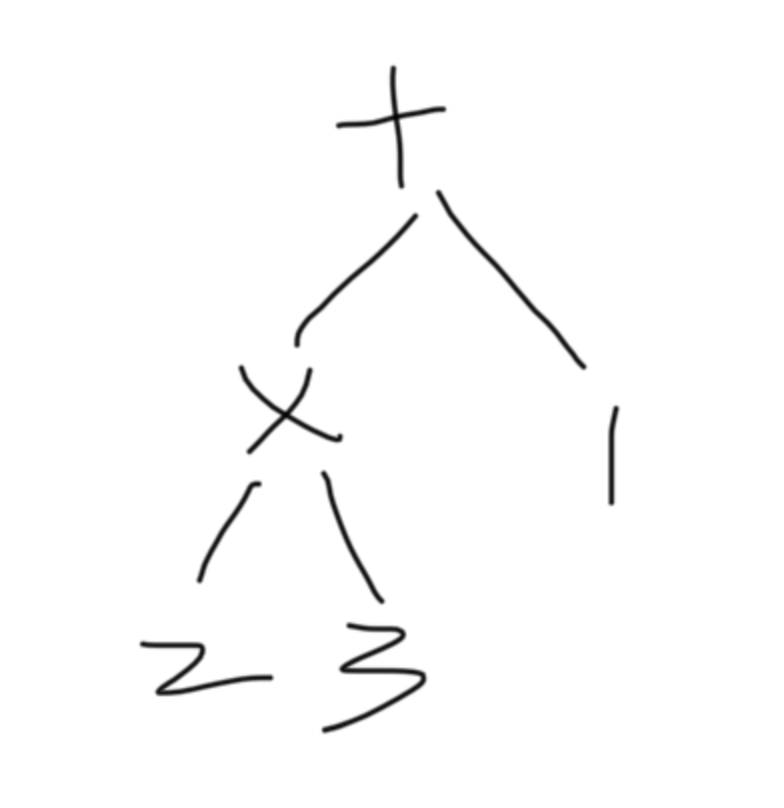
例如： $2\times3+1$

扫描到+时，op栈顶是乘号x，根据运算符的优先级，要先计算 $2\times3$ 这个乘法表达式；在表达式树中，进行中序遍历时，也要先遍历+的左子树（计算左子树的值）。因此要先弹栈，计算值，再将+存入op栈中。

同理，要是优先级相等，相同优先级的运算是从左向右进行的，仍然可以先计算值。

反之，若优先级小于当前运算符，例如： $2+1\times3$ ，扫描到x时，直接入op栈。扫描完毕后，再依次弹出，计算值即可。

代码

以下是代码模板，eval()函数是独立开的，涉及到别的运算，例如乘方、取余数等都可以用这套模板，更改eva()函数，再做细节调整即可。

#include <iostream>
#include <stack>
#include <unordered_map>

using namespace std;

stack<int> num; // 数字栈
stack<char> op; // 操作栈
// 计算值
void eval() {    // 取出num栈顶的两个元素A、B；和op栈顶的操作符o
    // 先入栈的为A，后入栈的为B，计算表达式A o B的值，并将值存入num栈
    int b = num.top(); num.pop();
    int a = num.top(); num.pop();
    int ans;
    char o = op.top(); op.pop();
    if (o == '+') ans = a + b;
    else if (o == '-') ans = a - b;
    else if (o == '*') ans = a * b;
    else ans = a / b;
    num.push(ans);
}

int main() {
    // 计算符号的优先级
    unordered_map<char, int> pr{{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}}; 
    string str;
    cin >> str;
    
    for (int i = 0; i < str.size(); ++ i) {
        char ch = str[i];
        if (isdigit(ch)) { // 若扫描到数字，考虑到数字可能占用多位
            int x = 0, j = i;
            while (j < str.size() && isdigit(str[j])) {
                x = x * 10 + (str[j ++] - '0');
            }
            i = j - 1;
            num.push(x);
        }
        else if (ch == '(') op.push(ch);
        else if (ch == ')') {
            while (op.top() != '(') eval();
            op.pop(); // 将（弹出栈
        }
        else { // + - * / 等计算符号
            while (!op.empty() && op.top() != '(' && pr[op.top()] >= pr[ch]) eval();
            op.push(ch);
        }
    }
    while (!op.empty()) eval();
    cout << num.top() << endl;
    
    return 0;
}

1106. 解析布尔表达式

update@2022年11月 5日星期六 15时48分20秒 CST

问题描述

分析

和中缀表达式求值原理是类似的，都是用两个栈（一个操作数栈nums和一个操作符栈ops），解决表达式求值问题

本题相对简单，无需考虑运算优先级的问题

以下分析摘自@宫水三叶的Leetcode题解
从前往后处理 s，根据当前处理的字符为何值进行分情况讨论：
,：分隔符，直接跳过；
t 或 f：操作数，添加到 nums 栈中；
|、& 或 !：操作符，添加到 ops 栈中；
(：子表达式的左端点，为了在我们从「双栈」中取出数值和符号计算时，可以知道某个子表达式计算完成，需要记录一下。往 nums 追加一个占位符号 - 来代指；
)：子表达式的右端点，代表一个子表达式的结束。可从「双栈」中取出符号和数组进行计算（在 ops 中仅取栈顶元素，代表当前子表达式的操作符；而在 nums 中则取到代表左端点的占位元素 - 为止），并将结果重新放入 nums 中。

代码实现

java版完整代码

class Solution {
    public boolean parseBoolExpr(String expression) {
        Deque<Character> nums = new LinkedList<>(), ops = new LinkedList<>();
        for (char ch : expression.toCharArray()) {
            if (ch == ',') continue;
            if (ch == 't' || ch == 'f') nums.push(ch);
            if (ch == '&' || ch == '|' || ch == '!') ops.push(ch);
            if (ch == '(') nums.push('(');
            if (ch == ')') {
                // 
                char cur = ' ', op = ops.pop();
                while (!nums.isEmpty() && nums.peek() != '(') {
                    char top = nums.pop();
                    cur = cur == ' ' ? top : cal(cur, top, op);
                }
                if (op == '!') cur = cur == 't' ? 'f' : 't';
                nums.pop(); nums.push(cur);
            }
        }
        return nums.peek() == 't';
    }
    // 计算 a OP b = ?
    // & | 
    // !看作 & 即可
    public char cal(char a, char b, char op) {
        boolean x = a == 't', y = b == 't';
        boolean ans = (op == '|') ? (x | y) : (x & y);
        return ans ? 't' : 'f';
    }
}

150. 逆波兰表达式求值

逆波兰表达式又称后缀表达式，由波兰的逻辑学家卢卡西维兹提出。其特点是，没有括号，运算符号紧跟在与之相关的操作数后边

求后缀表达式的值

示例 1：

输入：tokens = ["2","1","+","3","*"]
输出：9
解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

计算后缀表达式比较简单，由于操作符紧跟在与之相关的操作数后边，无需考虑运算符号的优先级问题。这样，采用一个操作数栈即可解决问题

java代码

class Solution {
    public int evalRPN(String[] tokens) {
        // 后缀表达式 只需借助一个操作数栈即可
        Deque<Integer> nums = new LinkedList<>();
        for (String str : tokens) {
            int num = 0;
            if (Character.isDigit(str.charAt(0)) || str.length() > 1) {
                num = Integer.parseInt(str);
                nums.push(num);
            } else { // 操作符
                int y = nums.pop(), x = nums.pop();
                int cur = 0;
                switch(str) {
                    case "+": cur = x + y; break;
                    case "-": cur = x - y; break;
                    case "*": cur = x * y; break;
                    case "/": cur = x / y; break; 
                }
                nums.push(cur);
            }
        }
        return nums.pop();   
    }
}

中缀表达式转化为后缀表达式

中缀转后缀，加上后缀表达式求值其实就组成了完整的中缀表达式求值

只需借助操作符栈，原理同求解中缀表达式一模一样

/**
* 题目要求：
* 中缀表达式转化为后缀表达式
* 表达式中只包含 + - * / % 五种运算
*
* 示例1：
* 中缀表达式 7 % ((10 * 3 + 1 + 2) * 2 - 3) - (3 * (4 - 10)) + 8
* 后缀表达式 7 10 3 * 1 + 2 + 2 * 3 - %  3 4 10 - * - 8 +
*/

完整代码

import java.util.*;

public class Main {
    public static void main(String[] args) {
        // 中缀表达式转后缀表达式

        /**
         * 题目要求：
         * 中缀表达式转化为后缀表达式
         * 表达式中只包含 + - * / % 五种运算
         *
         * 示例1：
         * 中缀表达式 7 % ((10 * 3 + 1 + 2) * 2 - 3) - (3 * (4 - 10)) + 8
         * 后缀表达式 7 10 3 * 1 + 2 + 2 * 3 - %  3 4 10 - * - 8 +
         */
        String myCase = "7 % ((10 * 3 + 1 + 2) * 2 - 3) - (3 * (4 - 10)) + 8".replace(" ", "");
        Deque<Character> ops = new LinkedList<>();
        List<String> res = new ArrayList<>();
        char[] chars = myCase.toCharArray();
        int n = chars.length;
        // 优先级
        int[] priority = new int[128];
        priority['+'] = 1;
        priority['-'] = 1;
        priority['*'] = 2;
        priority['/'] = 2;
        priority['%'] = 2;
        for (int i = 0; i < n; i++) {
            char ch = chars[i];
            // 数字直接加入
            if (Character.isDigit(ch)) {
                int j = i, x = 0;
                while (j < n && Character.isDigit(chars[j])) {
                    x = 10 * x + (chars[j++] - '0');
                }
                i = j - 1;
                res.add(Integer.toString(x));
            } else if (ch == '(') ops.push(ch);
            else if (ch == ')') {
                while (ops.peek() != '(') res.add(String.valueOf(ops.pop()));
                ops.pop(); // 弹出 ( 左括号
            } else { // 是运算符号
                while (!ops.isEmpty() && priority[ops.peek()] >= priority[ch]) res.add(String.valueOf(ops.pop()));
                ops.push(ch);
            }
        }
        while (!ops.isEmpty()) res.add(String.valueOf(ops.pop()));
        for (String ch : res) {
            System.out.print(ch + " ");
        }
        System.out.println();
    }
}

1597. 根据中缀表达式构造二叉表达式树

题目描述

二叉表达式树 是一种表达算术表达式的二叉树。二叉表达式树中的每一个节点都有零个或两个子节点。叶节点（有 0 个子节点的节点）表示操作数，非叶节点（有 2 个子节点的节点）表示运算符： '+' （加）、 '-' （减）、 '*' （乘）和 '/' （除）。

对于每一个运算符为 op 的非叶节点，对应的 中缀表达式 为 (A op B)，其中 A 是左子树所表达的表达式， B 是右子树所表达的表达式。

给定一个 中缀表达式 字符串 s，其中包含操作数、上面提到的运算符，以及括号 '(' 与 ')' 返回一个有效的 二叉表达式树，其 中序遍历 序列对应表达式 s 消除括号后的序列

注意，表达式的一般解析顺序适用于 s，即优先解析括号内的表达式，然后解析乘除法，最后解析加减法。

同时，操作数在 s 和树的中序遍历中 出现顺序相同 。

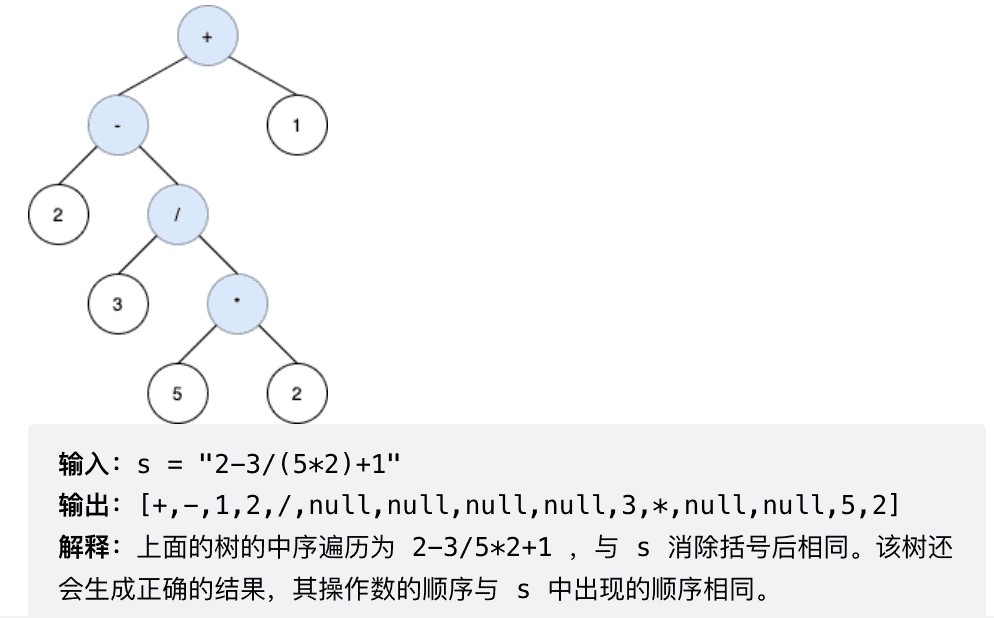
示例

简要分析

没什么特别的，多增加一个栈用来保存Node节点即可

代码

class Solution {
    public Node expTree(String ss) {
       Deque<Character> ops = new LinkedList<>();
       Deque<Integer> nums = new LinkedList<>();
       Deque<Node> st = new LinkedList<>();
       var s = ss.toCharArray();
       int n = s.length;
       int[] pr = new int[128];
       pr['+'] = 1; pr['-'] = 1;
       pr['*'] = 2; pr['/'] = 2;
       for (int i = 0; i < n; ++i) {
            char t = s[i];
            if (isDigit(t)) {
            // 如果允许数字大于9的话。本题弱化了要求
            //    int num = 0, j = i;
            //    while (j < n && isDigit(s[j])) {
            //        num = num * 10 + s[j++] - '0';
            //    }
            //    i = j - 1;
            //    nums.push(num);
            //    st.push(new Node((char)(num + '0')));
                nums.push(t - '0');
                st.push(new Node(t));
            } else if (t == '(') ops.push(t); // 左括号直接入栈
            else if (t == ')') {
                // 遇到右括号，计算和上一个左括号之间表达式的值 "(subExpr)"
                while (ops.peek() != '(') eval(ops, nums, st);
                ops.pop(); // 弹出左括号
            } else {
                // 如果当前运算符的优先级小于等于上一个运算符
                // 例如： 1+2+3 6*9+3
                // 要先计算上一个表达式「x ops y」的值
                while (!ops.isEmpty() && pr[t] <= pr[ops.peek()]) eval(ops, nums, st);
                ops.push(t);
            }
        } 
        while (!ops.isEmpty()) {
            eval(ops, nums, st);
        }
        return st.peek();
    } 
    void eval(Deque<Character> ops, Deque<Integer> nums, Deque<Node> st) {
        int y = nums.pop(), x = nums.pop();
        Node nodeY = st.pop(), nodeX = st.pop();
        char op = ops.pop();
        int ans = 0;
        Node cur = null;
        switch(op) {
            case '-':
                ans = x - y;
                cur = new Node('-');
                break;
            case '+':
                ans = x + y;
                cur = new Node('+');
                break;
            case '*':
                ans = x * y;
                cur = new Node('*');
                break;
            case '/':
                ans = x / y;
                cur = new Node('/');
                break;
        } 
        nums.push(ans);
        cur.left = nodeX;
        cur.right = nodeY;
        st.push(cur);
        return;
    }
    boolean isDigit(char x) {
        return x >= '0' && x <= '9';
    }
}