素数计数

简要分析总结判定质数的几种方法，从直观判定到埃氏筛，再到线性筛（欧拉筛）

质数，又称素数，是指在大于1的自然数中，只有1和它本身两个正因数的数；如果除了1和它本身，还可以被其他自然数字整除，则称作合数。

规定1既不是质数也不是合数。

判定一个数是否为质数

求解isPrime(x)方法

按照定义

最直观的思路就是按照定义来，遍历小于x的所有数字（大于1），如果有数字可以整除x，则x为合数，否则就是质数

boolean iSPrime(int x) {
    if (x < 2) return false; // 0, 1 
    for (int i = 2; i < x; ++i) {
        if (x % i == 0) return false;
    }
    return true;  
}

优化

上述直观思路的时间复杂度为 $\Omicron(n)$ 的

大于1的最小自然数是2，因此可以不用遍历到x-1，只需遍历2,3,4,...,x // 2，检查是否有数字可以整除x即可

但是这样做整体效率仍然是 $\Omicron(n)$ ，只是常数小一点

是否可以继续减小遍历的长度？

假设 $x$ 为合数，不妨设 $x=p*q$ ，根据定义，因子 $p,q$ 满足 $1 < p <= q$ （令p为较小者），由于 $x = \sqrt{x}*\sqrt{x}$

因此较小者 $p <= \sqrt{x}$

综上，只需检查 $2,3,4\dots,\sqrt{x}$，中是否存在数字可以整除 $x$ ，如果不存在，$x$ 就是质数

boolean iSPrime(int x) {
    if (x < 2) return false;
    for (int i = 2; i * i <= x; ++i) { // 乘法代替除法
        if (x % i == 0) return false;
    }
    return true;  
}

时间复杂度为 $\Omicron(\sqrt{n})$

---

如果现在要求出 $[2,n)$ 范围内的所有质数，用上述方法去挨个判断，总体时间复杂度为 $\Omicron(n\sqrt{n})$

这里介绍两个效率的更高的算法

埃氏筛

埃拉托斯特尼筛法，sieve of Eratosthenes，简称埃氏筛

算法简介

埃氏筛的关键点在于：

如果 $x$ 为质数，则 $x$ 的倍数，即 $2x,3x,4x,...$ 一定不是质数

每一次确定 $x$ 为质数后，直接筛去其倍数的数字

算法实现时，创建两个数组

• $primes[]$ 用来保存所有的质数
• $sieved[]$ 用来保存被筛除的合数

遍历 $[2,n]$：

• 如果当前数字 $x$ 不是合数，加入到 $primes[]$ 中去；筛去 $x$ 的倍数
• 优化点：$x$ 的倍数 $2x,3x,...,x*x,...$ ，其中 $[2x, 3x,...,x*x)$ 部分肯定已经被 $2，3$ 等质数筛掉了，为避免重复计算，我们可以直接从 $x*x$ 开始

代码实现

public int[] getPrimes(int n) {
    int[] primes = new int[n];
    int idx = 0;
    boolean[] sieved = new boolean[n + 1];
    for (int x = 2; x < n; ++x) {
        if (!sieved[x]) {
            primes[idx++] = x;
            for (int j = x; j < n / x; ++j) { // 防止溢出写法
                sieved[x * j] = true;
            }
        }
    }
    int[] ans = new int[idx];
    System.arraycopy(primes, 0, ans, 0, idx);
    return ans;
}

复杂度分析

复杂度分析要抓住核心语句（程序中最深，执行最多次）的执行次数量级，很显然，该算法中需要分析筛合数的执行次数 sieved[x * j] = true

不难得到 $h(n) = \sum_{2 <=p<=n}\frac{n}{p}$ ，其中 $p$ 为质数

参考为什么埃式筛法的时间复杂度是O(nloglogn)？

根据Mertens’ theorems，$\lim_{n \rightarrow \infty}{(\sum_{p\le n}^{}{\frac{1}{p} }-\ln \ln n-M)}=0, M\approx 0.2614972$ ，所以上述算法的时间复杂度为 $O(nlog⁡log⁡n)$ 。

论文地址为Mertens’ Proof of Mertens’ Theorem

线性筛

算法分析

埃氏筛的效率很优秀，但是也存在问题：一个合数可能会被多个质数筛选到，也就是存在重复筛选的问题

例如：合数18，会被2和3先后筛掉

如何避免一个合数被重复筛选呢？

线性筛，又叫欧拉筛，提出一种思路：一个合数只允许被其最小的质因子筛除

不同于埃氏筛，线性筛对于每个自然数都进行筛选过程，分别筛去当前自然数 $x$ 和质数集合 $primes[j]$ 中的每一个质数的乘积，直到 x % primes[j] == 0 跳出循环

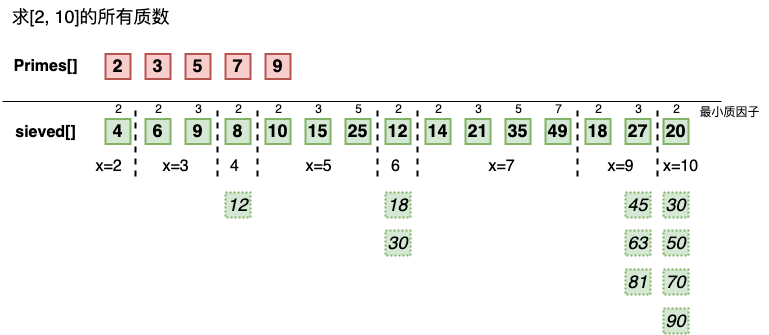
下面模拟了线性筛求解 $[2,10)$ 之间的所有质数的流程，参见动画

在整个算法，精髓在于 if (x % primes[j] == 0) break; 这一句，它保证了合数 $num$ 只会被其最小质因子筛去

为什么？

当前扫描到质数primes[j]，如果x % primes[j] == 0，记k = x / primes[j]

假设不跳出，接下来要筛除的合数为 x * primes[t] = num，t > j

因为x = k * primes[j]

(k * primes[t]) * primes[j] = x * primes[t] = num

primes[t]一定不是num的最小质因子，因为prines[]单调增，t > j，primes[j] < primes[t]，所以此时，没必要筛去num。

实际上由于单调特性，此时的primes[j]就是num=x*primes[t],t>j的最小质因子

代码实现

class Solution {
    public int countPrimes(int n) {
        int[] primes = new int[n];
        int idx = 0;
        boolean[] sieved = new boolean[n + 1];
        for (int x = 2; x < n; ++x) {
            if (!sieved[x]) primes[idx++] = x;
            for (int j = 0; j < idx && primes[j] * x < n; ++j) {
                sieved[x * primes[j]] = true;
                if (x % primes[j] == 0) break;
            }
        }
        return idx;
    }
}

由于每个合数只会被筛选一次，整体时间复杂度为 $\Omicron(n)$

下面贴出求解 $[2,10]$ 内所有质数的整体流程