前缀和与差分

发表于 更新于 分类于 Artalk： loading...

前缀和、差分，二维前缀和、二维差分

一维前缀和

简概

image-20211013162713182

用空间换时间

s[0]一般设为0，s[k]表示前k个元素的和。对应到数组下标上就是0~k-1

第l个到第r个元素[l,r]的和即为，s[r] - s[l - 1]

代码模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <iostream>

using namespace std;

int main() {
    int n, m;
    cin >> n >> m;
    int q[n], s[n + 1];
    s[0] = 0;
    for (int i = 0; i < n; ++ i) {
        cin >> q[i];
        s[i + 1] = s[i] + q[i];
    }
    
    for (int i = 0; i < m; ++ i) {
        int l, r;
        cin >> l >> r;
        int res = s[r] - s[l - 1];
        cout << res << endl;
    }
    return 0;
}

二维前缀和

acwing 798. 子矩阵的和

简概

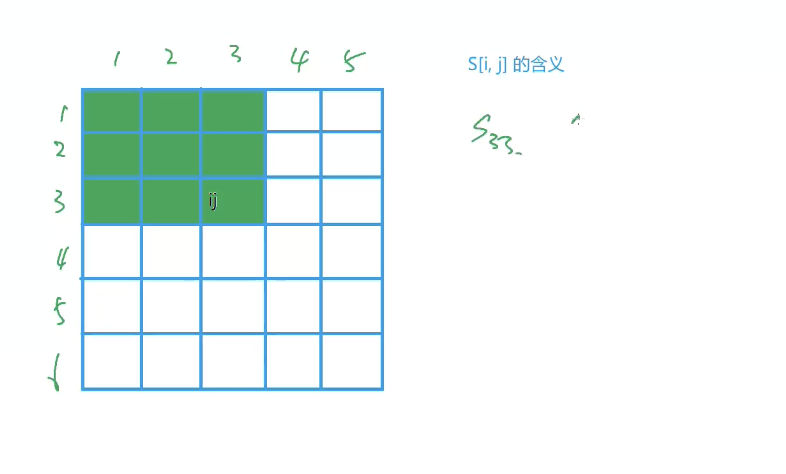
s[i][j]代表二维前缀和，[i,j]代表坐标

image-20211023120055687

考虑问题：

1、s[i][j]如何计算？

对于问题1，前缀和数组

s[i,j] = s[i-1,j] + s[i,j-1] - s[i-1,j-1] + a[i,j]

2、(x1,y1),(x2,y2)这一子矩阵中所有的数字和如何计算？

公式：

子矩阵的和 = s[x2, y2] - s[x1-1, y2] - s[x2, y1-1] + s[x1-1, y1-1]

很好理解。画图如下

image-20211023130140860

代码模板

acwing 798. 子矩阵的和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <iostream>
#include <vector>

using namespace std;

int main() {
    int n, m, q;
    cin >> n >> m >> q;
    int qs[n][m];
  
    vector<vector<int>> prefixSum(n + 1, vector<int>(m + 1, 0));
    for (int i = 0; i < n; ++ i) {
        for (int j = 0; j < m; ++ j) {
            cin >> qs[i][j];
        }
    }
    // 计算二维前缀和数组prefixSum
    for (int i = 0; i < n; ++ i) {
        for (int j = 0; j < m; ++ j) {
            prefixSum[i + 1][j + 1] = prefixSum[i][j + 1] + prefixSum[i + 1][j] - prefixSum[i][j] + qs[i][j];
        }
    }
    
    while (q --) {
        // 计算被（x1，y1）和（x2， y2）包住的子矩阵的和
        int x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        int res = 0;
        // 计算公式
        res = prefixSum[x2][y2] - prefixSum[x1 - 1][y2] - prefixSum[x2][y1 - 1] + prefixSum[x1 - 1][y1 - 1];
        cout << res << endl;
    }
    
    return 0;
}

差分

简概

差分–可以简单地理解是前缀和的逆运算。

已知数组 a1,a1,a3…ana_1,a_1,a_3\dots a_n

构造数组 bnb_n

使得 an=b1+b2+⋯+bna_n = b_1 + b_2 +\dots +b_n

构造方法

b1=a1;b_1 = a_1;

b2=a2−a1;b_2 = a_2 - a_1;

b3=a3−a2;b_3 = a_3 - a_2;

⋮\vdots

bn=an−an−1;b_n = a_n - a_{n-1};

差分有什么用？

快速处理一种操作：

在[an][a_n]数组内[l, r]范围内所有数，全部加上c：a1+c,a2+c……an+ca_1 + c, a_2 + c……a_n + c

如果常规操作，遍历[an][a_n]数组，需要O(n)时间复杂度

现在可以这么操作：

bl+cb_l + c 则 al,al+1,…ar…ana_l,a_{l+1},\dots a_r\dots a_n 都会加上c，接下来，如果只保证[l, r]区间内的数加c，则$b_{r+1} −-c$即可。

总结

ana_n[l, r]内的元素加c

bl+cb_l+c

br+1−cb_{r+1}-c

只用O(1)的时间就可以给原数组加上某一个固定的值。

image-20211029184942123

acwing 797.差分

代码模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <iostream>

using namespace std;

int main() {
    int n, m;
    cin >> n >> m;
    int q[n];
    for (int i = 0; i < n; ++ i) {
        cin >> q[i];
    }
    // 构造差分数组 b_n
    int b[n];
    b[0] = q[0];
    for (int i = 1; i < n; ++ i) {
        b[i] = q[i] - q[i - 1];
    }
    while (m --) {
        int l, r, c;
        cin >> l >> r >> c;
        b[l - 1] += c;
        b[r] -= c;
    }

    for (int i = 0; i < n; ++ i) {
        if(i) b[i] += b[i - 1];
        printf("%d ", b[i]);
    }
    return 0;
}

参考yxc版本，将构造[bn][b_n]数组过程和加c操作 合并一起

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <iostream>

using namespace std;

int q[100001];
int b[100001];

void insert(int l, int r, int x) {
    b[l] += x;
    b[r + 1] -= x;
}

int main() {
    int n, m;
    cin >> n >> m;
    for (int i = 0; i < n; ++ i) {
        cin >> q[i];
        insert(i, i, q[i]);
    }
    // 构造差分数组 b_n
    while (m --) {
        int l, r, c;
        cin >> l >> r >> c;
        insert(l - 1, r - 1, c);
    }

    for (int i = 0; i < n; ++ i) {
        if(i) b[i] += b[i - 1];
        printf("%d ", b[i]);
    }
    return 0;
}

例题

1109. 航班预订统计

这里有 n 个航班，它们分别从 1 到 n 进行编号。

有一份航班预订表 bookings ，表中第 i 条预订记录 bookings[i] = [firsti, lasti, seatsi] 意味着在从 firsti 到 lasti （包含 firsti 和 lasti ）的 每个航班 上预订了 seatsi 个座位。

请你返回一个长度为 n 的数组 answer，里面的元素是每个航班预定的座位总数。

示例

1
2
3
4
5
6
7
8
9
输入：bookings = [[1,2,10],[2,3,20],[2,5,25]], n = 5
输出：[10,55,45,25,25]
解释：
航班编号        1   2   3   4   5
预订记录 1 ：   10  10
预订记录 2 ：       20  20
预订记录 3 ：       25  25  25  25
总座位数：      10  55  45  25  25
因此，answer = [10,55,45,25,25]

本题属于「区间修改+单点查询」，是差分的标准应用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int[] corpFlightBookings(int[][] bs, int n) {
        int[] c = new int[n + 1];
        int[] res = new int[n];
        for (int[] tt : bs) {
            int l = tt[0] - 1, r = tt[1] - 1, val = tt[2];
            c[l] += val;
            c[r + 1] -= val;
        }
        res[0] = c[0];
        for (int i = 1; i < n; ++i) {
            res[i] = res[i - 1] + c[i];
        }
        return res;
    }
}

二维差分

798.差分矩阵

简概

同理，二维差分相当于二维前缀和的逆运算。

[an][a_n]相当于是数组[bn][b_n]的二维前缀和

[bn][b_n]是二维差分数组

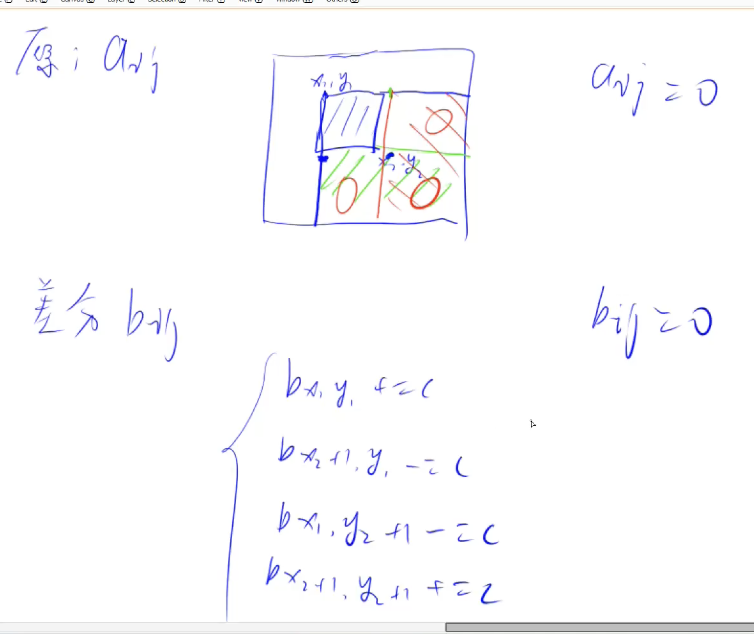
给二维的子矩阵中每一个数加一个值c

bx1,y1+=cb_{x_1,y_1} += c

bx2+1,y1−=cb_{x_2+1,y_1} -= c

bx1,y2+1−=cb_{x_1,y_2+1} -= c

bx2+1,y2+1+=cb_{x_2+1,y_2+1} += c

image-20211029195819171

代码模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <iostream>

using namespace std;

// n行m列
int n, m, q;
const int N = 1010;

int a[N][N];
int b[N][N];

void insert(int x1, int y1, int x2, int y2, int c) {
    b[x1][y1] += c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

int main() {
    scanf("%d%d%d", &n, &m, &q);
    for (int i = 1; i <= n; ++ i) {
        for (int j = 1; j <= m; ++ j) {
            scanf("%d", &a[i][j]);
            insert(i, j, i, j, a[i][j]);
        }
    }
    
    while (q --) {
        int x1, y1, x2, y2, c;
        scanf("%d%d%d%d%d", &x1, &y1, &x2, &y2, &c);
        insert(x1, y1, x2, y2, c);
    }
    for (int i = 1; i <= n; ++ i) {
        for (int j = 1; j <= m; ++ j) {
            // 求二维前缀和数组公式
            b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
            printf("%d ", b[i][j]);
        }
        printf("\n");
    }
    
    return 0;
}

📔博文图谱

提及本博文的链接