关于并查集

发表于 更新于 Artalk： loading...

实现功能：

  1. 合并两个集合
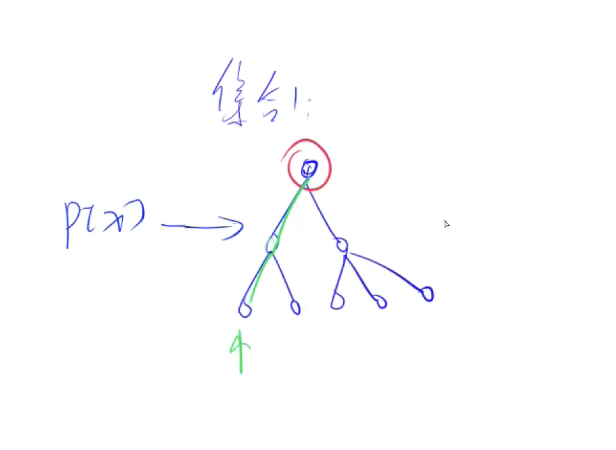
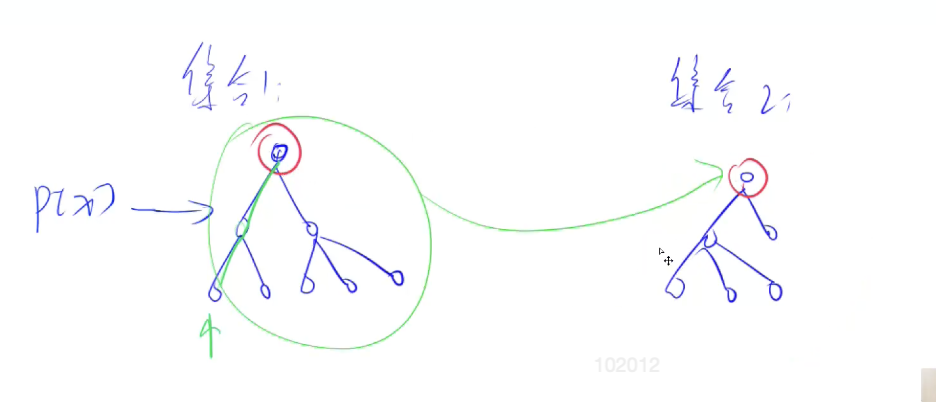
  2. 查询两个元素是否在一个集合中

时间复杂度近乎O（1）

基本原理：

用树的形式维护所有集合：

//

根结点的编号即–> 当前集合的编号

每个节点的p(x)存储的是x的父节点

image-20211016085824315

问题1：如何判断是否是树根

1
if(p(x) == x)

问题2：如何求x的集合编号 *

循环寻找根节点

1
while (p[x] != x)    x = p[x];

问题3：如何合并两个集合?

加边

​ 例如：px是x的集合编号，py是y的集合编号。p[x] = y （默设 x是根节点

​ 直接将x所在的集合插到y那儿去。

image-20211016090801617

优化：

针对问题2*

路径压缩：遍历一次后，将路径上的节点直接指向根节点

p[x] = root

还有个按秩压缩，不常用

代码实现：

acwing 836.合并集合

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <iostream>
#include <vector>

using namespace std;

const int N = 1e5+10;
int p[N];

// 返回x的祖宗节点（根节点） + 路径压缩
// 关键方法
int find(int x) {
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main() {
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; ++ i) {
        p[i] = i;
    }
    while (m --) {
        char op[2];
        int a, b;
        cin >> op >> a >> b;
        if (op[0] == 'M') p[find(a)] = find(b);
        else {
            if (find(a) == find(b)) puts("Yes");
            else puts("No");
        }
    }
    return 0;
}

find函数中的判断语句是灵活的，根据具体情况随机应变。

1
2
3
4
int find(int x) {
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

注意与下题中的find函数进行比较

例题：

128. 最长连续序列

问题描述：

给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。

请你设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例1：

1
2
3
输入：nums = [100,4,200,1,3,2]
输出：4
解释：最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    unordered_map<int, int> p;
    // 路径压缩 
    int find(int x) {
        if (p.count(x)) return p[x] = find(p[x]);
        else return x;
    }
    // 并查集实现 O(n)时间复杂度
    int longestConsecutive(vector<int>& nums) {    
        // 初始，将每个数字x的祖宗节点设置为下一个数字x+1 （因为要求连续的序列）
        // find函数实现的是，将x的祖宗节点设置为 数组中存在的 以x起 连续增长的（x+1） 最大值的 下一个 ——（find函数中，查找下去，如果不存在的话，返回的是输入x，也就是 存在的最大值 的下一个）
        
        for (auto x : nums) {
            p[x] = x + 1;
        }
        int ans = 0;
        for (auto x : nums) {
            int tmp = find(x);
            ans = max(ans, tmp - x);
        }
        return ans;
    }
};

这里之所以用哈希表，是要利用unordered_map::count函数，要判断查找的数字节点是否在数组中存在。

📔博文图谱

提及本博文的链接