「转载」字典树/前缀树的实现
前言
本文完全转载自路漫漫我不畏在leetcode 208. 实现 Trie (前缀树)一题中的题解
介绍 Trie
Trie [traɪ] 读音和 try 相同,它的另一些名字有:字典树,前缀树,单词查找树等。
专业解释参见wiki百科
Trie 是一颗非典型的多叉树模型,多叉好理解,即每个结点的分支数量可能为多个。
为什么说非典型呢?因为它和一般的多叉树不一样,尤其在结点的数据结构设计上,比如一般的多叉树的结点是这样的:
1 | struct TreeNode { |
而 Trie 的结点是这样的(假设只包含’a’~'z’中的字符):
1 | struct TrieNode { |
要想学会 Trie 就得先明白它的结点设计。我们可以看到TrieNode结点中并没有直接保存字符值的数据成员,那它是怎么保存字符的呢?
这时字母映射表next的妙用就体现了,TrieNode* next[26]中保存了对当前结点而言下一个可能出现的所有字符的链接,因此我们可以通过一个父结点来预知它所有子结点的值:
1 | for (int i = 0; i < 26; i++) { |
我们来看个例子吧。
想象以下,包含三个单词 “sea”,“sells”,“she” 的 Trie 会长啥样呢?
它的真实情况是这样的:

Trie 中一般都含有大量的空链接,因此在绘制一棵单词查找树时一般会忽略空链接,同时为了方便理解我们可以画成这样:
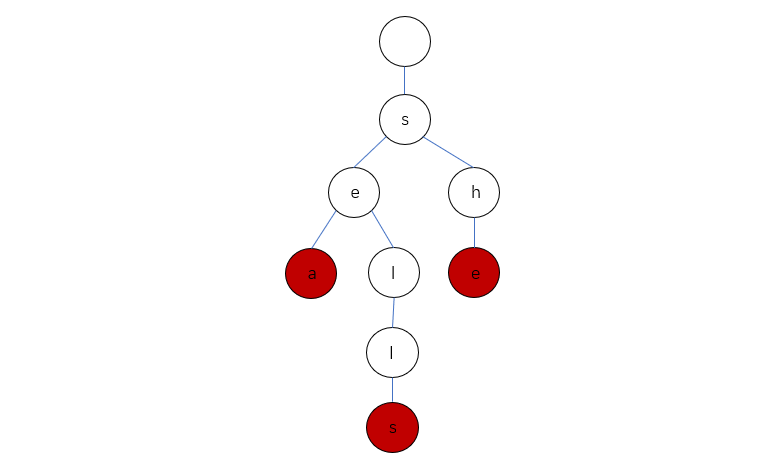
接下来我们一起来实现对 Trie 的一些常用操作方法。
操作方法
定义类 Trie
1 | class Trie { |
插入
描述:向Trie中插入一个单词word
实现:这个操作和构建链表很像。首先从根结点的子结点开始与word第一个字符进行匹配,一直匹配到前缀链上没有对应的字符,这时开始不断开辟新的结点,直到插入完word的最后一个字符,同时还要将最后一个结点isEnd = true;,表示它是一个单词的末尾。
1 | void insert(string word) { |
查找
描述:查找Trie中是否存在单词word
实现:从根结点的子结点开始,一直向下匹配即可,如果出现结点值为空就返回false,如果匹配到了最后一个字符,那我们只需判断 node->isEnd即可。
1 | bool search(string word) { |
前缀匹配
描述:判断Trie中是或有以prefix为前缀的单词
实现:和search操作类似,只是不需要判断最后一个字符结点的isEnd,因为既然能匹配到最后一个字符,那后面一定有单词是以它为前缀的。
1 | bool startsWith(string prefix) { |
总结
通过以上介绍和代码实现我们可以总结出 Trie 的几点性质:
Trie 的形状和单词的插入或删除顺序无关,也就是说对于任意给定的一组单词,Trie 的形状都是唯一的。
查找或插入一个长度为 L 的单词,访问 next 数组的次数最多为 L+1,和 Trie 中包含多少个单词无关。
Trie 的每个结点中都保留着一个字母表,这是很耗费空间的。如果 Trie 的高度为 n,字母表的大小为 m,最坏的情况是 Trie 中还不存在前缀相同的单词,那空间复杂度就为
最后,关于 Trie 的应用场景,希望你能记住 8 个字:一次建树,多次查询。(慢慢领悟叭~~)
相关例题
合集->字典树
677. 键值映射
1 | class TrieNode { |
📔博文图谱
提及本博文的链接