acwing算法基础课笔记-区间合并

发表于 更新于 分类于 Artalk： loading...

前言

将一些有交集的区间进行合并，这里记录一个比较快速的实现方式。

若两个区间只有端点相交，也认为可以合并

Ex：[1,3] [3,10]

例题

acwing 803. 区间合并

问题描述：

给定 n 个区间 [li,ri][l_i,r_i]，要求合并所有有交集的区间。

注意如果在端点处相交，也算有交集。

输出合并完成后的区间个数。

例如：[1,3] 和 [2,6] 可以合并为一个区间 [1,6]。

输入格式

第一行包含整数 n。

接下来 n 行，每行包含两个整数 l 和 r。

输出格式

共一行，包含一个整数，表示合并区间完成后的区间个数。

数据范围

1≤n≤1000001≤n≤100000
−109≤li≤ri≤109−10^9≤l_i≤r_i≤10^9

输入样例：

1
2
3
4
5
6
5
1 2
2 4
5 6
7 8
7 9

解题思路

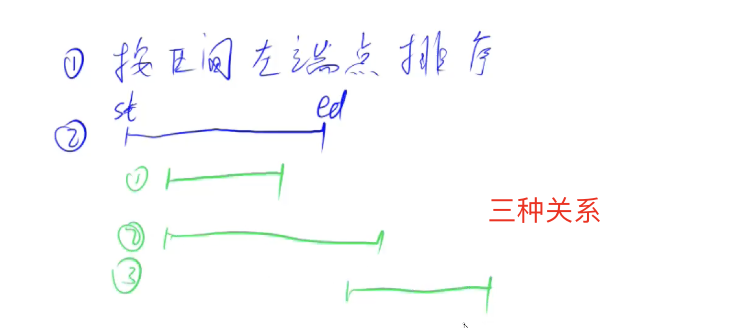
  • 按区间左端点排序

  • 扫描所有区间，将可能有交集的区间合并

    • 每次维护一个“当前”的区间 st[__________] ed

    • 扫描到第i个区间，与当前区间有三种关系：

      • 在当前区间内部
      • 有交集
      • 无交集
      image-20211110144229505

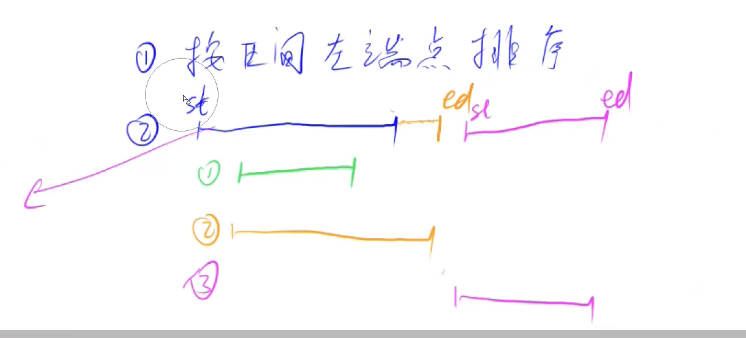
  • 针对不同情况：

    • 在维护的区间内部时，st和ed不变

    • 若有交集，则ed后移，即维护的区间变长

    • 若无交集，则将现在维护的区间放入最终结果，并将第i个区间作为当前维护的区间

    image-20211110144656250

过程图示：

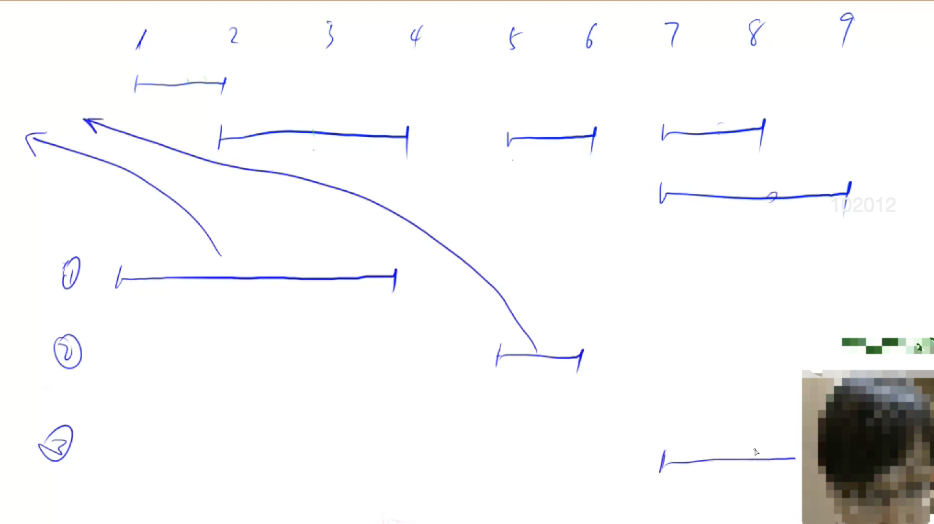
image-20211110145126527

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

typedef pair<int, int> PII;
const int N = 1e5+10;

int n;
vector<PII> segs;

void merge(vector<PII> &segs) {
    vector<PII> res;
    sort(segs.begin(), segs.end()); // 优先以PII.first进行排序，即按照左端点排序
    int st = -2e9, ed = -2e9; // 设置边界范围
    for (auto seg : segs) {
        if (ed < seg.first) { // 对应第三种情况
            if (st != -2e9) res.emplace_back({st, ed}); // 判断一下是否是初始区间
            st = seg.first, ed = seg.second;
        }
        else ed = max(ed, seg.second); // 对应第二种情况 和第一种情况
    }
    if (st != -2e9) res.emplace_back({st, ed}); // 将最后一个区间加到结果里面去 
    // 判断是防止 输入的数组是空的
    segs = res; // 更新segs
}

int main() {
    
    return 0;
}