图论：最短路径问题-Dijkstra

发表于 2022-07-04 更新于 2022-07-14 分类于 acwing算法基础课笔记 Artalk： loading...

最短路 Dijkstra

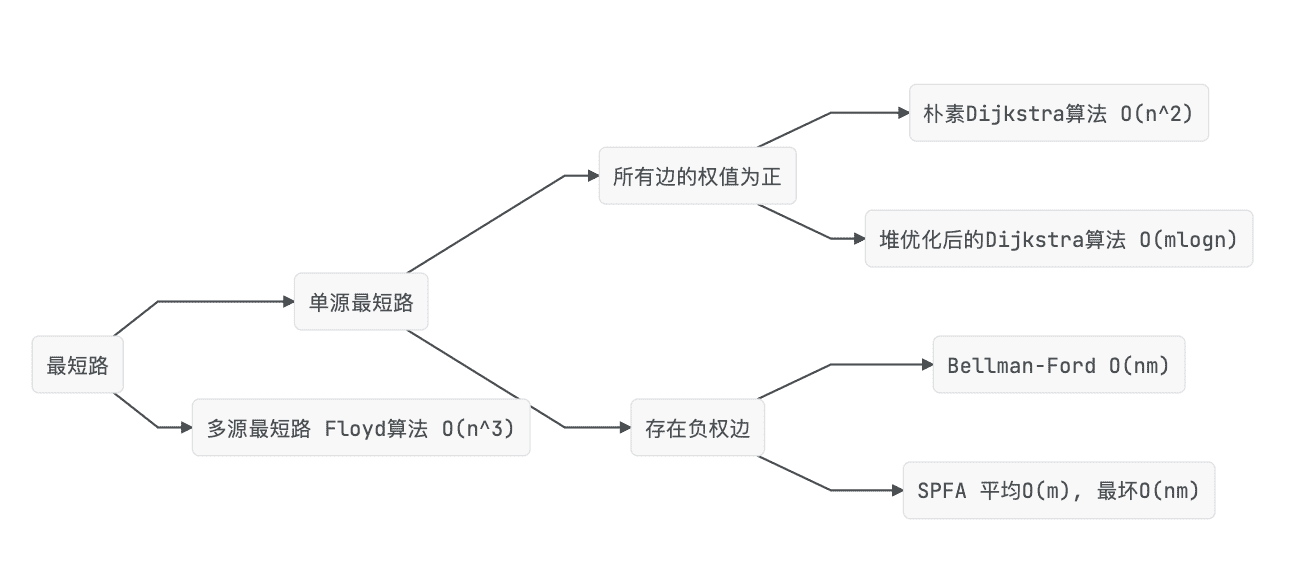
最短路问题，可以分为单源最短路径和多源最短路径问题

所有边的权值为正的情况下，可以使用 $\text{Dijkstra}$ 算法

$n$ 为点的数量， $m$ 为边的数量

存在负权边，可以使用

Bellman Ford，可以解决「有边数限制」的最短路
SPFA，判断负环

Dijkstra算法

求源点到其他所有点的距离的最小值

时间复杂度为 $\Omicron{(n^2)}$

算法流程

1.初始化距离数组 $Dist[]$ ，源点到源点距离为0，其余赋为 $\text{INF}$

维持一个集合 $\text{S}$ ，保存着已求出最短距离的节点

2.迭代 $\text{n - 1}$ 次：

找到尚未加入集合 $S$ 中的，距离源点最近的点 $t$ ，加入集合 $S$ 中
然后用新加入的点 $t$ 更新源点到其他点的距离
即比较 $Dist\{orig\to \text{the others}\}$ 和 $Dist\{orig\to t \to \text{the others}\}$ 哪个更小
这一步被称为「松弛操作」
如何形象地理解最短路算法中“松弛”的含义？ - 李欣宜的回答 - 知乎

算法证明

$\text{Dijkstra}$ 算法中，每一轮迭代后，将点 $ver$ 加入集合 $S$ ，此时

$dist[ver]=\text{shortest distance of}\ <orig\to ver>$

可以用反证法证明：

如果此时至少存在一个尚未加入集合 $S$ 的 $t$ ，使得 $Dist\{orig\to t\to ver\}<Dist\{orig\to ver\}$

则 $Dist\{orig\to t\} < Dist\{orig\to ver\}$ ，那么节点 $t$ 应当已经加入了集合 $S$ ，与假设不符合，证毕

值得注意的是

在 $Dist\{orig\to t\to ver\}<Dist\{orig\to ver\}$ 的情况下，如果边 $edge<t\to ver>$ 权值为负，是推不出来 $Dist\{orig\to t\} < Dist\{orig\to ver\}$ 的

这也就是为什么 $\text{Dijkstra}$ 算法只能适用于所有边的权值为正的图

代码实现

算法核心代码

ps：以下代码是针对稠密图，采用邻接矩阵存储

int[] dijkstra() {
    Arrays.fill(dist, INF);
    dist[1] = 0; // 源点
    for (int i = 1; i < n; ++i) {
        int t = -1;
        // 找出尚未加到集合S中，且距离最近的点
        for (int j = 1; j <= n; ++j) {
            if (!st[j] && (t == -1 || dist[j] < dist[t])) t = j;
        }
        // 用新加入的点t更新dist数组
        for (int j = 1; j <= n; ++j) {
            dist[j] = Math.min(dist[j], dist[t] + g[t][j]);
        }
        st[t] = true;
    }
    return dist;
}

java版完整代码

acwing 849. Dijkstra求最短路 I

求1号点到n号点的最短距离

import java.util.*;
import java.io.*;

class Main{
    static final int INF = 0x3f3f3f3f;
    static BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
    static final int N = 510;
    static int[][] g = new int[N][N];
    static boolean[] st = new boolean[N];
    static int[] dist = new int[N];
    static int n, m;
    static int dijkstra() {
        for (int i = 1; i < n; ++i) {
            int t = -1;
            for (int j = 1; j <= n; ++j) {
                if (!st[j] && (t == -1 || dist[j] < dist[t])) t = j;
            }
            for (int j = 1; j <= n; ++j) {
                dist[j] = Math.min(dist[j], dist[t] + g[t][j]);
            }
            st[t] = true;
        }
        return dist[n] == INF ? -1 : dist[n];
    }
    public static void main(String[] args) throws Exception {
        String[] tt = cin.readLine().split(" ");
        n = Integer.parseInt(tt[0]);
        m = Integer.parseInt(tt[1]);
        String[] strs;
        int a, b, w;
        for (int i = 0; i < n; ++i) Arrays.fill(g[i+1], INF);
        for (int i = 0; i < m; ++i) {
            strs = cin.readLine().split(" ");
            a = Integer.parseInt(strs[0]); b = Integer.parseInt(strs[1]); w = Integer.parseInt(strs[2]);
            g[a][b] = Math.min(g[a][b], w);
        }
        Arrays.fill(dist, INF);
        dist[1] = 0;
        System.out.println(dijkstra());
        
        cin.close();
    }
}

C++代码

const int N = 510;

int n, m;
int g[N][N];
int dist[N];
bool st[N];

int dijkstra()
{
    memset(dist, 0x3f, sizeof dist); // 初始化为INF值
    dist[1] = 0; // 1为源点

    for (int i = 0; i < n - 1; i ++ )
    {
        int t = -1; // 表示还没找到最近的点
        for (int j = 1; j <= n; j ++ )
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;

        for (int j = 1; j <= n; j ++ )
            dist[j] = min(dist[j], dist[t] + g[t][j]); // 用t更新到其他点的距离

        st[t] = true; // 将t点加入集合S
    }

    if (dist[n] == 0x3f3f3f3f) return -1; // 源点和n点是不连通的
    return dist[n];
}

堆优化

优化思路

整个算法步骤中

寻找最小距离是 $\Omicron(n^2)$ 的，可以用堆存储距离，优化为 $\Omicron(n)$ （每一次是 $\Omicron(1)$ 的）

使用堆存储距离后，单次修改操作是 $\Omicron(\log{n})$ 的，一共修改 $m$ 次

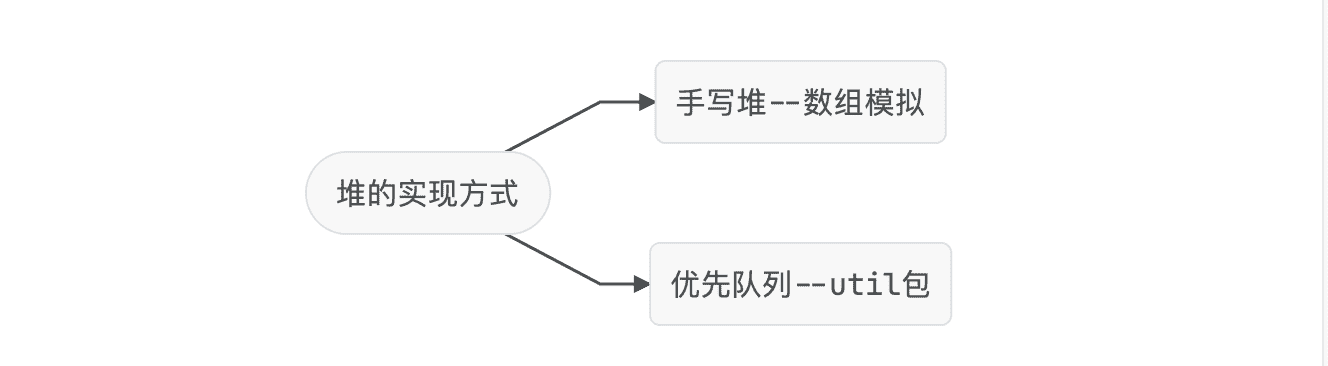
具体实现

使用优先队列，由于优先队列不支持修改元素，需要更新距离时，直接插入一个新元素。这样，优先队列中可能会有 $m$ 个元素，因此总复杂度为 $\Omicron(m\log m)$
用数组模拟可以修改任意元素的堆，需要做映射，实现繁琐，代码参见模拟堆

复杂度分析

在图中，边的数量 $m$ 最多为 $n*(n$ - $1)$ ，数量级为 $n^2$

$m\log{m} = \Theta(m\log{n^2})$

且 $m\log{n^2}=2m\log{n}$ ，因此 $m\log n = \Theta(m\log m)$ ，使用JDK自带的优先队列即可

代码

算法核心代码

ps：邻接表方式存储图

int[] dijkstra() {
    Arrays.fill(dist, INF);
    dist[1] = 0;
    PriorityQueue<int[]> heap = new PriorityQueue<>(n, (a,b) -> {return a[1] - b[1];}); // lambda重写compare方法
    heap.offer(new int[]{1, 0}); // heap中存储的是节点序号和到源点距离
    while (!heap.isEmpty()) {
        int[] cur = heap.poll();
        int ver = cur[0]; int distance = cur[1];
        if (st[ver]) continue; // 已经加入S集合则跳过
        st[ver] = true; // 将当前节点加入S集合
        for (int i = h[ver]; i != -1; i = ne[i]) {
            int j = e[i]; // 获取节点序号
            if (dist[j] > distance + w[i]) { // 更新
                dist[j] = distance + w[i]; 
                heap.offer(new int[]{j, dist[j]}); // 不修改，直接插入更新后的距离
            }
        }
    }
    return dist;
}

java版完整代码

acwing 850. Dijkstra求最短路 II

import java.util.*;
import java.io.*;

class Main{
    static final int INF = 0x3f3f3f3f;
    static BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
    static final int N = (int) 150010;
    static int[] e = new int[N];
    static int[] ne = new int[N];
    static int[] h = new int[N];
    static int[] w = new int[N];
    static int idx;
    static boolean[] st = new boolean[N];
    static int[] dist = new int[N];
    static int n, m;
    static void add(int a, int b, int c) {
        e[idx] = b; w[idx] = c; ne[idx] = h[a]; h[a] = idx++;
    } 
    
    static int dijkstra() {
        Arrays.fill(dist, INF);
        dist[1] = 0;
        PriorityQueue<int[]> heap = new PriorityQueue<>(n, (a,b) -> {return a[1] - b[1];});
        heap.offer(new int[]{1, 0}); // heap中存储的是节点序号和到源点距离
        while (!heap.isEmpty()) {
            int[] cur = heap.poll();
            int ver = cur[0]; int distance = cur[1];
            if (st[ver]) continue;
            st[ver] = true;
            for (int i = h[ver]; i != -1; i = ne[i]) {
                int j = e[i];
                if (dist[j] > distance + w[i]) {
                    dist[j] = distance + w[i];
                    heap.offer(new int[]{j, dist[j]});
                }
            }
        }
        return dist[n] == INF ? -1 : dist[n];
    }
    
    public static void main(String[] args) throws Exception {
        String[] strs = cin.readLine().split("\\s+");
        n = Integer.parseInt(strs[0]);
        m = Integer.parseInt(strs[1]);
        
        int a, b, w;
        Arrays.fill(h, -1);
        for (int i = 0; i < m; ++i) {
            strs = cin.readLine().split("\\s+");
            a = Integer.parseInt(strs[0]); b = Integer.parseInt(strs[1]); w = Integer.parseInt(strs[2]);
            add(a, b, w);
        }
        System.out.println(dijkstra());
        
        cin.close();
    }
}

C++完整代码

acwing 850. Dijkstra求最短路 II

#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>

using namespace std;

typedef pair<int, int> PII;

const int N = 1e6 + 10;

int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dist[N];
bool st[N];

void add(int a, int b, int c)
{    // w[] 存权重
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    priority_queue<PII, vector<PII>, greater<PII>> heap;
    heap.push({0, 1});

    while (heap.size())
    {
        auto t = heap.top();
        heap.pop();

        int ver = t.second, distance = t.first;

        if (st[ver]) continue;
        st[ver] = true;

        for (int i = h[ver]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > dist[ver] + w[i])
            {
                dist[j] = dist[ver] + w[i];
                heap.push({dist[j], j});
            }
        }
    }

    if (dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

int main()
{
    scanf("%d%d", &n, &m);

    memset(h, -1, sizeof h);
    while (m -- )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }

    cout << dijkstra() << endl;

    return 0;
}

📔博文图谱

提及本博文的链接

Prim算法–最小生成树