图论：单源最短路径问题-Bellma ford

图存在负权边的情况下，可以使用Bellman Ford算法和最短路径快速算法Shortest Path Faster Algorithm, SPFA

迭代 $k$ 次后，此时 $dist[i]$ 数组表示从源点经过不超过 $k$ 条边到顶点 $i$ 的最短距离

Bellman Ford算法

$n$ 代表图的顶点数量， $m$ 代表图的边的数量

时间复杂度 $\Omicron(nm)$

算法流程

迭代 $\text{n - 1}$ 次

• 遍历所有的边 $edge<a\to b>$ ，执行松弛操作
• 更新 $\text{dist}$ 数组， $dist[b] = min\{dist[b],\ dist[a] + weight<a\to b>\}$

算法意义

关于迭代次数

迭代 $k$ 次后，此时 $dist[i]$ 数组表示从源点经过不超过 $k$ 条边到顶点 $i$ 的最短距离

换句话说，第 $k$ 次迭代时，如果 $dist[i]$ 数组某些点更新了，说明存在长度为 $k$ 的最短路径

此原理可用来检测一个图是否存在「负权回路」

例如，第 $n$ 次迭代时，如果 $dist[]$ 数组中 $dist[2]$ 更新了，说明存在长度为 $n$ 的 $orig\to 2$ 的最短路径

路径长度为 $n$ ，即 $n$ 条边，意味着路径上有 $n+1$ 个点，根据抽屉原理，此路径一定存在环，且一定是负权环

ps: 检测负权回路，一般用 $\text{SPFA}$ 算法来做

Tips

1.

全部更新完毕后，对于任意的边 $edge<a\to b>$

均存在 $dist[b] \le dist[a] + weight<a\to b>$

上述不等式也称作「三角不等式」

2.

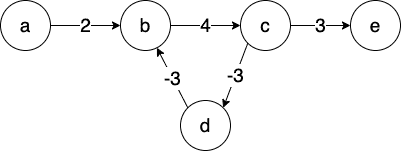
如果存在「负权回路」，最短路径可能不存在

例如：

从 $\text{a}$ 到 $\text{e}$ ，最短路径长度理论上是 $-\infty$

3.

一般来说，SPFA优于Bellman Ford算法

但是Bellman Ford可以用来解决「有边数限制」的最短路径问题

代码实现

核心代码

注意，每次迭代开始前，要先对 $dist[]$ 数组进行备份

避免松弛操作时，使用本轮迭代更新后的 $dist[]$ 数组

原理同动态规划：使用滚动数组降低空间占用#注意事项

以下是邻接表存储的实现方式

int[] bellmanFord() {
    // 初始化dist数组
    Arrays.fill(dist, INF);
    dist[1] = 0;
    for (int i = 0; i < k; ++i) {
        backup = Arrays.copyOf(dist, n + 1); // 备份dist数组
        // 遍历所有的边
        // 执行松弛操作
        for (int j = 1; j <= n; ++j) {
            for (int t = h[j]; t != -1; t = ne[t]) {
                int a = j, b = e[t], c = w[t];
                dist[b] = Math.min(dist[b], backup[a] + c);
            }
        }
    }
    return dist;
}

有边数限制的最短路问题

acwing 853. 有边数限制的最短路

给定一个 $n$ 个点 $m$ 条边的有向图，图中可能存在重边和自环，边权可能为负数。

请你求出从 $1$ 号点到 $n$ 号点的最多经过 $k$ 条边的最短距离，如果无法从 $1$ 号点走到 $n$ 号点，输出 impossible。

注意：图中可能存在负权回路

import java.util.*;
import java.io.*;

class Main{
    static final int N = 510;
    static final int M = 10010;
    static final int INF = 0x3f3f3f3f;
    static int[] h = new int[N];
    static int[] e = new int[M];
    static int[] ne = new int[M];
    static int[] w = new int[M];
    static int idx;
    static int[] dist = new int[N];
    static int[] backup = new int[N];
    static int n, m, k;
    static BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
    public static void main(String[] args) throws Exception {
        String[] str = cin.readLine().split("\\s+");
        n = Integer.parseInt(str[0]); m = Integer.parseInt(str[1]); k = Integer.parseInt(str[2]);
        int a, b, c;
        Arrays.fill(h, -1);
        for (int i = 0; i < m; ++i) {
            str = cin.readLine().split("\\s+");
            a = Integer.parseInt(str[0]); b = Integer.parseInt(str[1]); c = Integer.parseInt(str[2]);
            add(a, b, c);
        }
        
        bellmanFord();
       
        cin.close();
    }
    static void bellmanFord() {
        
        Arrays.fill(dist, INF);
        dist[1] = 0;
        for (int i = 0; i < k; ++i) {
            backup = Arrays.copyOf(dist, n + 1);
            for (int j = 1; j <= n; ++j) {
                for (int t = h[j]; t != -1; t = ne[t]) {
                    int a = j, b = e[t], c = w[t];
                    dist[b] = Math.min(dist[b], backup[a] + c);
                }
            }
        }
        if (dist[n] > INF / 2) System.out.println("impossible");
        else System.out.println(dist[n]);
    }
    static void add(int a, int b, int c) {
        e[idx] = b;
        ne[idx] = h[a];
        w[idx] = c;
        h[a] = idx++;
    }
}

---

📔博文图谱

提及本博文的链接

• 图论：最短路径问题-Dijkstra

• 图论：单源最短路径问题-SPFA