图论：建图&搜索

发表于 更新于 Artalk： loading...
图的邻接表实现 DFS BFS

本文重点在于代码实现

相关文章见笔记: acwing算法基础课笔记-搜索与图论

建图

邻接表法

为节点A添加一条指向节点B的边

A→B\text{A}\to \text{B}

A节点的值为a，B节点同理

此处节点的值=节点的索引

1
2
3
4
5
void add(int a, int b) {
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

DFS-深度优先遍历

1
2
3
4
5
6
7
8
9
void dfs(int u) {
    visited[u] = true;
    for (int i = h[u]; i != -1; i = ne[i]) {
        int val = e[i];
        if (!visited[val]) {
            dfs(val);
        }
    }
}

BFS-广度优先遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void bfs(int u) {
    Queue<Integer> q = new LinkedList<>();
    q.offer(u);
    while (!q.isEmpty()) {
        int size = q.size();
        while (size-- > 0) {
            int cur = q.poll();
            for (int i = h[cur]; i != -1; i = ne[i]) {
                int val = e[i];
                if (!visited[val]) {
                    q.offer(val);
                    visited[val] = true;
                }
            }
        }
    }
}

几处细节

🌰

首先，关于各个数组的含义

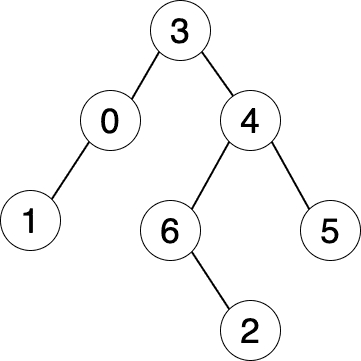
以下默认节点序号即为节点的值，例如

treeNode.drawio

h[N]，数组的索引为：节点序号，数组的值为：该节点的“全局地址idx“

e[M]，索引为：全局地址idx，值：节点序号

ne[M]，索引为：全局地址idx，值：全局地址idx

visited[N]，索引为：节点序号，值：true/false表示该节点是否被访问过

🌰

无向图，构建的时候，需要增加 a→ba\to b 的边，也要增加 b→ab\to a 的边，M=2∗mM=2*m

🌰

h[N] 存储的是每个邻接表的表头地址，初始化时，均为-1，Arrays.fill(h, -1)。可以用来判断链表的终止

关于链表的模拟，查看笔记数组模拟单双链表

例题

863. 二叉树中所有距离为 K 的结点

先将二叉树转为图，再进行 BFS\text{BFS}

1
2
3
4
5
6
7
8
9
10
11
12
13
public void build(TreeNode root) {
    if (root == null) return;
    if (root.left != null) {
        add(root.val, root.left.val);
        add(root.left.val, root.val);
        build(root.left);
    }
    if (root.right != null) {
        add(root.val, root.right.val);
        add(root.right.val, root.val);
        build(root.right);
    }
}

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
class Solution {
    static final int N = 510;
    static final int M = 2 * N;
    int idx = 0;
    int[] h = new int[N];
    int[] ne = new int[M];
    int[] e = new int[M];
    boolean[] visited = new boolean[N];
    void add(int a, int val) {
        e[idx] = val;
        ne[idx] = h[a];
        h[a] = idx++;
    }
    public List<Integer> distanceK(TreeNode root, TreeNode target, int k) {
        Arrays.fill(h, -1);
        idx = 0;
        build(root);
        int tt = target.val;
        visited[tt] = true;
        Queue<Integer> q = new LinkedList<>();
        q.offer(tt);
        List<Integer> res = new ArrayList<>();
        while (!q.isEmpty() && k >= 0) {
            int size = q.size();
            while (size-- > 0) {
                int cur = q.poll();
                if (k == 0) {
                    res.add(cur);
                    continue;
                }
                for (int i = h[cur]; i != -1; i = ne[i]) {
                    if (!visited[e[i]]) {
                        q.offer(e[i]);
                        visited[e[i]] = true;
                    }
                }
            }
            k--;
        }
        return res;
    }

    public void build(TreeNode root) {
        if (root.left != null) {
            add(root.val, root.left.val);
            add(root.left.val, root.val);
            build(root.left);
        }
        if (root.right != null) {
            add(root.val, root.right.val);
            add(root.right.val, root.val);
            build(root.right);
        }
    }
}